用随机缺失的普查指标进行量差估计。
IF 1.2
3区 数学
Q3 MATHEMATICS, INTERDISCIPLINARY APPLICATIONS
引用次数: 0
摘要
本文定义了当数据为右删失且删失指标随机缺失时的分布函数估计量,并建立了它们的强表示和渐近正态性。此外,基于经验似然法,我们分别定义了存在和不存在辅助信息时的最大经验似然估计值和两样本量差的平滑对数经验似然比,并证明了它们的渐近分布。通过仿真研究和实际数据分析,研究了所提方法的有限样本行为。本文章由计算机程序翻译,如有差异,请以英文原文为准。
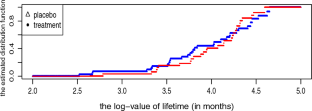
Quantile difference estimation with censoring indicators missing at random.
In this paper, we define estimators of distribution functions when the data are right-censored and the censoring indicators are missing at random, and establish their strong representations and asymptotic normality. Besides, based on empirical likelihood method, we define maximum empirical likelihood estimators and smoothed log-empirical likelihood ratios of two-sample quantile difference in the presence and absence of auxiliary information, respectively, and prove their asymptotic distributions. Simulation study and real data analysis are conducted to investigate the finite sample behavior of the proposed methods.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Lifetime Data Analysis
数学-数学跨学科应用
CiteScore
2.30
自引率
7.70%
发文量
43
审稿时长
3 months
期刊介绍:
The objective of Lifetime Data Analysis is to advance and promote statistical science in the various applied fields that deal with lifetime data, including: Actuarial Science – Economics – Engineering Sciences – Environmental Sciences – Management Science – Medicine – Operations Research – Public Health – Social and Behavioral Sciences.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


