平行轴矩形和圆形线圈的互感计算

IF 16.4 1区化学 Q1 CHEMISTRY, MULTIDISCIPLINARY

Accounts of Chemical Research Pub Date : 2023-11-21 DOI:10.1049/elp2.12396

Dongze Yu, Baichao Chen, Yao Luo, Xinglong Zhou, Yue Yu, Xinyi Yang, Yike Xiang

{"title":"平行轴矩形和圆形线圈的互感计算","authors":"Dongze Yu, Baichao Chen, Yao Luo, Xinglong Zhou, Yue Yu, Xinyi Yang, Yike Xiang","doi":"10.1049/elp2.12396","DOIUrl":null,"url":null,"abstract":"<p>Simple and practical methods have been provided for the mutual inductance between rectangular and circular coils with parallel axes. The 2D Integral solution is given for the coils without the axial overlap. To improve the efficacy of the proposed approach for the partial or full axial overlap, the series solution derived by the truncated region eigenfunction expansion (TREE) is provided. Both integral and TREE expressions show very high accuracy through comparison with the finite element method simulation and experiment results. Numerical comparisons reveal that the TREE solution is the most efficient while keeping sufficient accuracy, and it is also applicable to all sorts of coil positions.</p>","PeriodicalId":1,"journal":{"name":"Accounts of Chemical Research","volume":null,"pages":null},"PeriodicalIF":16.4000,"publicationDate":"2023-11-21","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://onlinelibrary.wiley.com/doi/epdf/10.1049/elp2.12396","citationCount":"0","resultStr":"{\"title\":\"Mutual inductance calculation for rectangular and circular coils with parallel axes\",\"authors\":\"Dongze Yu, Baichao Chen, Yao Luo, Xinglong Zhou, Yue Yu, Xinyi Yang, Yike Xiang\",\"doi\":\"10.1049/elp2.12396\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>Simple and practical methods have been provided for the mutual inductance between rectangular and circular coils with parallel axes. The 2D Integral solution is given for the coils without the axial overlap. To improve the efficacy of the proposed approach for the partial or full axial overlap, the series solution derived by the truncated region eigenfunction expansion (TREE) is provided. Both integral and TREE expressions show very high accuracy through comparison with the finite element method simulation and experiment results. Numerical comparisons reveal that the TREE solution is the most efficient while keeping sufficient accuracy, and it is also applicable to all sorts of coil positions.</p>\",\"PeriodicalId\":1,\"journal\":{\"name\":\"Accounts of Chemical Research\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":16.4000,\"publicationDate\":\"2023-11-21\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://onlinelibrary.wiley.com/doi/epdf/10.1049/elp2.12396\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Accounts of Chemical Research\",\"FirstCategoryId\":\"5\",\"ListUrlMain\":\"https://onlinelibrary.wiley.com/doi/10.1049/elp2.12396\",\"RegionNum\":1,\"RegionCategory\":\"化学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"CHEMISTRY, MULTIDISCIPLINARY\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Accounts of Chemical Research","FirstCategoryId":"5","ListUrlMain":"https://onlinelibrary.wiley.com/doi/10.1049/elp2.12396","RegionNum":1,"RegionCategory":"化学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"CHEMISTRY, MULTIDISCIPLINARY","Score":null,"Total":0}

引用次数: 0

摘要

为平行轴的矩形和圆形线圈之间的互感提供了简单实用的方法。对于无轴向重叠的线圈，给出了二维积分解法。为了提高所提方法对部分或全部轴向重叠的有效性，我们提供了通过截断区域特征函数展开（TREE）得出的串联解。通过与有限元法模拟和实验结果的比较，积分表达式和 TREE 表达式都显示出非常高的精度。数值比较表明，TREE 解法在保持足够精度的同时效率最高，而且适用于各种线圈位置。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

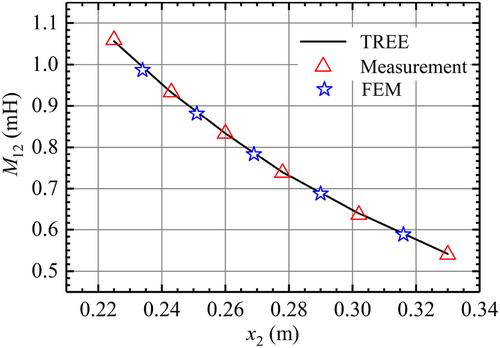
Mutual inductance calculation for rectangular and circular coils with parallel axes

查看原文本刊更多论文

Mutual inductance calculation for rectangular and circular coils with parallel axes

Simple and practical methods have been provided for the mutual inductance between rectangular and circular coils with parallel axes. The 2D Integral solution is given for the coils without the axial overlap. To improve the efficacy of the proposed approach for the partial or full axial overlap, the series solution derived by the truncated region eigenfunction expansion (TREE) is provided. Both integral and TREE expressions show very high accuracy through comparison with the finite element method simulation and experiment results. Numerical comparisons reveal that the TREE solution is the most efficient while keeping sufficient accuracy, and it is also applicable to all sorts of coil positions.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Accounts of Chemical Research 化学-化学综合

CiteScore

31.40

自引率

1.10%

发文量

312

审稿时长

2 months

期刊介绍： Accounts of Chemical Research presents short, concise and critical articles offering easy-to-read overviews of basic research and applications in all areas of chemistry and biochemistry. These short reviews focus on research from the author’s own laboratory and are designed to teach the reader about a research project. In addition, Accounts of Chemical Research publishes commentaries that give an informed opinion on a current research problem. Special Issues online are devoted to a single topic of unusual activity and significance. Accounts of Chemical Research replaces the traditional article abstract with an article "Conspectus." These entries synopsize the research affording the reader a closer look at the content and significance of an article. Through this provision of a more detailed description of the article contents, the Conspectus enhances the article's discoverability by search engines and the exposure for the research.