Chern classes in equivariant bordism

We introduce Chern classes in 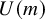$U(m)$-equivariant homotopical bordism that refine the Conner–Floyd–Chern classes in the 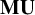$\mathbf {MU}$-cohomology of 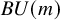$B U(m)$. For products of unitary groups, our Chern classes form regular sequences that generate the augmentation ideal of the equivariant bordism rings. Consequently, the Greenlees–May local homology spectral sequence collapses for products of unitary groups. We use the Chern classes to reprove the 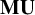$\mathbf {MU}$-completion theorem of Greenlees–May and La Vecchia.