混合维偏微分方程的完备性和有限元逼近
IF 1.7
3区 数学
Q3 COMPUTER SCIENCE, SOFTWARE ENGINEERING
引用次数: 0
摘要
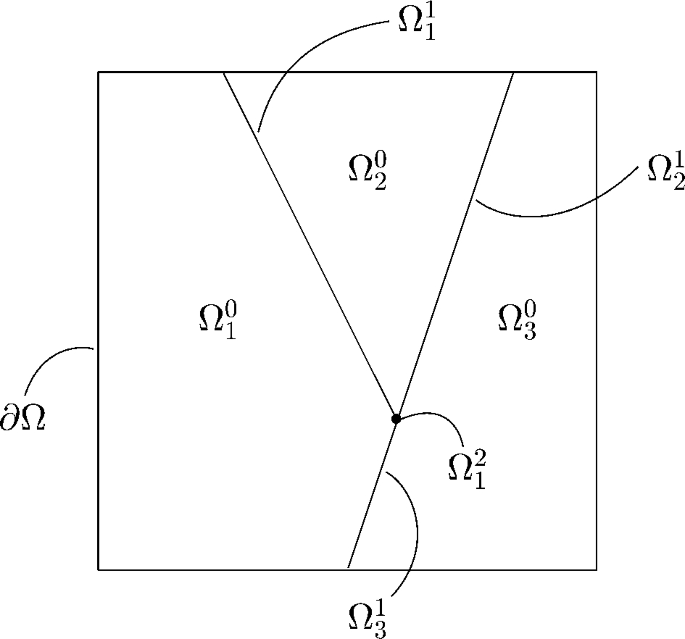
本文考虑了一个混合维度的椭圆偏微分方程,该方程是在一个具有大量嵌入界面的体域中提出的。文章特别研究了问题的好求和解的正则性。还提出了一种合适的有限元近似方法,并证明了先验误差约束。对于所产生的线性系统的求解,提出并分析了一种基于子空间分解的迭代方法。最后,还进行了数值实验,利用所提出的预条件器实现了快速收敛,证实了理论结论。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Well-posedness and finite element approximation of mixed dimensional partial differential equations
In this article, a mixed dimensional elliptic partial differential equation is considered, posed in a bulk domain with a large number of embedded interfaces. In particular, well-posedness of the problem and regularity of the solution are studied. A fitted finite element approximation is also proposed and an a priori error bound is proved. For the solution of the arising linear system, an iterative method based on subspace decomposition is proposed and analyzed. Finally, numerical experiments are presented and rapid convergence using the proposed preconditioner is achieved, confirming the theoretical findings.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

BIT Numerical Mathematics
数学-计算机:软件工程
CiteScore
2.90
自引率
0.00%
发文量
38
审稿时长
6 months
期刊介绍:
The journal BIT has been published since 1961. BIT publishes original research papers in the rapidly developing field of numerical analysis. The essential areas covered by BIT are development and analysis of numerical methods as well as the design and use of algorithms for scientific computing. Topics emphasized by BIT include numerical methods in approximation, linear algebra, and ordinary and partial differential equations.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


