有限深度液体表面毛细管波的精确解法
IF 0.5
Q3 MATHEMATICS
引用次数: 0
摘要
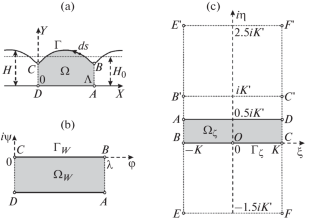
摘要 尝试用 Schwartz 函数方法重现著名的金纳斯利对有限深度液体表面毛细管波问题的精确解。然而,结果却得到了一个新的精确解,它与金纳斯利的解并不一致,尽管它是用雅克比椭圆函数的相同术语来表示的。本文介绍了对新解法进行独立数值验证的结果,证实了其可靠性。对该解法的参数分析表明,波长及其振幅与韦伯数之间存在非单调依赖关系。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Exact Solution for Capillary Waves on the Surface of a Liquid of Finite Depth
Abstract
An attempt was made to reproduce, using the Schwartz function method, the well-known exact solution of Kinnersley to the problem of capillary waves on the surface of a liquid of finite depth. However, as a result, a new exact solution was obtained, which does not coincide with the solution of Kinnersley, although it is expressed in the same terms of Jacobi elliptic functions. The results of an independent numerical verification of the new solution are presented, confirming its reliability. The parametric analysis of the solution revealed, in particular, a nonmonotonic dependence of the wavelength and its amplitude on the Weber number.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Russian Mathematics
MATHEMATICS-
CiteScore
0.90
自引率
25.00%
发文量
0
期刊介绍:
Russian Mathematics is a peer reviewed periodical that encompasses the most significant research in both pure and applied mathematics.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


