不可擦写字符的公共零点
IF 0.8
4区 数学
Q3 MATHEMATICS
引用次数: 0
摘要
我们研究有限群中不可还原字符之间的零共享行为。对于对称群 $\mathsf {S}_n$,除了一个例外,任何两个不可还字符都至少有一个公共零点。为了进一步探讨这一现象,我们引入了有限群 G 的公共零图,以 G 的非线性不可还原字符为顶点,并以边连接在某些公共群元素上消失的字符。我们证明,对于可解群和简单群,该图的连通分量数以三为界。最后,我们应用 $\mathsf {S}_n$ 的结果来证明由群的忠实不可还原字符诱导的排列上的度量的非等价性。本文章由计算机程序翻译,如有差异,请以英文原文为准。
COMMON ZEROS OF IRREDUCIBLE CHARACTERS
We study the zero-sharing behavior among irreducible characters of a finite group. For symmetric groups 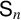 $\mathsf {S}_n$, it is proved that, with one exception, any two irreducible characters have at least one common zero. To further explore this phenomenon, we introduce the common-zero graph of a finite group G, with nonlinear irreducible characters of G as vertices, and edges connecting characters that vanish on some common group element. We show that for solvable and simple groups, the number of connected components of this graph is bounded above by three. Lastly, the result for
$\mathsf {S}_n$, it is proved that, with one exception, any two irreducible characters have at least one common zero. To further explore this phenomenon, we introduce the common-zero graph of a finite group G, with nonlinear irreducible characters of G as vertices, and edges connecting characters that vanish on some common group element. We show that for solvable and simple groups, the number of connected components of this graph is bounded above by three. Lastly, the result for 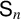 $\mathsf {S}_n$ is applied to prove the nonequivalence of the metrics on permutations induced from faithful irreducible characters of the group.
$\mathsf {S}_n$ is applied to prove the nonequivalence of the metrics on permutations induced from faithful irreducible characters of the group.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
1.70
自引率
0.00%
发文量
36
审稿时长
6 months
期刊介绍:
The Journal of the Australian Mathematical Society is the oldest journal of the Society, and is well established in its coverage of all areas of pure mathematics and mathematical statistics. It seeks to publish original high-quality articles of moderate length that will attract wide interest. Papers are carefully reviewed, and those with good introductions explaining the meaning and value of the results are preferred.
Published Bi-monthly
Published for the Australian Mathematical Society

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


