给定接触角的曲线域平均曲率流的最小运动格式及其计算

IF 1 3区数学 Q1 MATHEMATICS

Annali di Matematica Pura ed Applicata Pub Date : 2023-11-18 DOI:10.1007/s10231-023-01398-9

Tokuhiro Eto, Yoshikazu Giga

{"title":"给定接触角的曲线域平均曲率流的最小运动格式及其计算","authors":"Tokuhiro Eto, Yoshikazu Giga","doi":"10.1007/s10231-023-01398-9","DOIUrl":null,"url":null,"abstract":"<div><p>We introduce a capillary Chambolle-type scheme for mean curvature flow with prescribed contact angle. Our scheme includes a capillary functional instead of just the total variation. We show that the scheme is well-defined and has consistency with the energy minimizing scheme of Almgren–Taylor–Wang type. Moreover, for a planar motion in a strip, we give several examples of numerical computation of this scheme based on the split Bregman method instead of a duality method.</p></div>","PeriodicalId":8265,"journal":{"name":"Annali di Matematica Pura ed Applicata","volume":null,"pages":null},"PeriodicalIF":1.0000,"publicationDate":"2023-11-18","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://link.springer.com/content/pdf/10.1007/s10231-023-01398-9.pdf","citationCount":"0","resultStr":"{\"title\":\"On a minimizing movement scheme for mean curvature flow with prescribed contact angle in a curved domain and its computation\",\"authors\":\"Tokuhiro Eto, Yoshikazu Giga\",\"doi\":\"10.1007/s10231-023-01398-9\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div><p>We introduce a capillary Chambolle-type scheme for mean curvature flow with prescribed contact angle. Our scheme includes a capillary functional instead of just the total variation. We show that the scheme is well-defined and has consistency with the energy minimizing scheme of Almgren–Taylor–Wang type. Moreover, for a planar motion in a strip, we give several examples of numerical computation of this scheme based on the split Bregman method instead of a duality method.</p></div>\",\"PeriodicalId\":8265,\"journal\":{\"name\":\"Annali di Matematica Pura ed Applicata\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":1.0000,\"publicationDate\":\"2023-11-18\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://link.springer.com/content/pdf/10.1007/s10231-023-01398-9.pdf\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Annali di Matematica Pura ed Applicata\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s10231-023-01398-9\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Annali di Matematica Pura ed Applicata","FirstCategoryId":"100","ListUrlMain":"https://link.springer.com/article/10.1007/s10231-023-01398-9","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

本文介绍了具有规定接触角的平均曲率流的毛细管尚波勒型格式。我们的方案包括毛细管函数，而不仅仅是总变异。我们证明了该格式定义良好，并且与Almgren-Taylor-Wang型的能量最小化格式一致。此外，对于条带内的平面运动，我们给出了几个基于分裂Bregman方法而不是对偶方法的数值计算实例。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

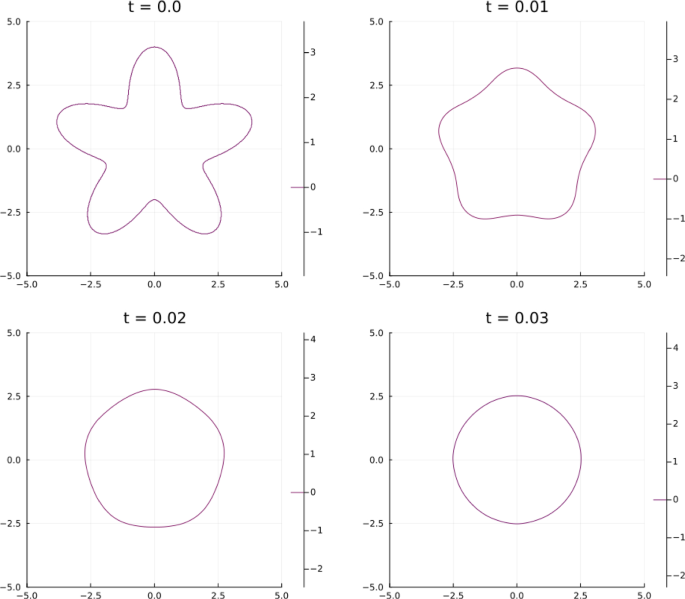
On a minimizing movement scheme for mean curvature flow with prescribed contact angle in a curved domain and its computation

查看原文本刊更多论文

On a minimizing movement scheme for mean curvature flow with prescribed contact angle in a curved domain and its computation

We introduce a capillary Chambolle-type scheme for mean curvature flow with prescribed contact angle. Our scheme includes a capillary functional instead of just the total variation. We show that the scheme is well-defined and has consistency with the energy minimizing scheme of Almgren–Taylor–Wang type. Moreover, for a planar motion in a strip, we give several examples of numerical computation of this scheme based on the split Bregman method instead of a duality method.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Annali di Matematica Pura ed Applicata 数学-数学

CiteScore

2.10

自引率

10.00%

发文量

审稿时长

>12 weeks

期刊介绍： This journal, the oldest scientific periodical in Italy, was originally edited by Barnaba Tortolini and Francesco Brioschi and has appeared since 1850. Nowadays it is managed by a nonprofit organization, the Fondazione Annali di Matematica Pura ed Applicata, c.o. Dipartimento di Matematica "U. Dini", viale Morgagni 67A, 50134 Firenze, Italy, e-mail annali@math.unifi.it). A board of Italian university professors governs the Fondazione and appoints the editors of the journal, whose responsibility it is to supervise the refereeing process. The names of governors and editors appear on the front page of each issue. Their addresses appear in the title pages of each issue.