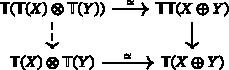
Algebraic theories of power operations

We develop and exposit some general algebra useful for working with certain algebraic structures that arise in stable homotopy theory, such as those encoding well-behaved theories of power operations for $E_{\infty }$ ring spectra. In particular, we consider Quillen cohomology in the context of algebras over algebraic theories, plethories, and Koszul resolutions for algebras over additive theories. By combining this general algebra with obstruction-theoretic machinery, we obtain tools for computing with $E_{\infty }$ algebras over $F_p$ and over Lubin–Tate spectra. As an application, we demonstrate the existence of $E_{\infty }$ periodic complex orientations at heights $h⩽2$.