莱斯利-高尔模型的图灵不稳定性
IF 1.1
4区 数学
Q1 MATHEMATICS
引用次数: 0
摘要
摘要本文研究了一个反应-扩散的Leslie-Gower捕食者-被食饵模型,该模型包含了种群内捕食、自扩散和交叉扩散。分析了解的长期行为,证明了吸收集的存在性。模式的存在性是通过寻找保证在没有扩散时稳定的平衡在允许扩散时变得不稳定的条件来研究的。本文章由计算机程序翻译,如有差异,请以英文原文为准。
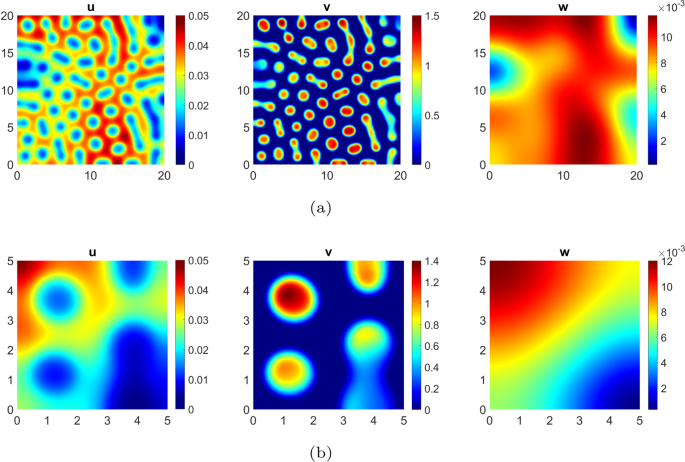
Turing instability for a Leslie–Gower model
Abstract The aim of this paper is to investigate a reaction-diffusion Leslie–Gower predator–prey model, incorporating the intraguild predation and both self and cross-diffusion. The longtime behaviour of the solutions is analysed, proving the existence of an absorbing set. The existence of patterns is investigated by looking for conditions guaranteeing that an equilibrium, stable in the absence of diffusion, becomes unstable when diffusion is allowed.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Ricerche di Matematica
Mathematics-Applied Mathematics
CiteScore
3.00
自引率
8.30%
发文量
61
期刊介绍:
“Ricerche di Matematica” publishes high-quality research articles in any field of pure and applied mathematics. Articles must be original and written in English. Details about article submission can be found online.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


