协同克里格的多种形式:多元空间估计量的多样性

IF 2.8 3区地球科学 Q2 GEOSCIENCES, MULTIDISCIPLINARY

Mathematical Geosciences Pub Date : 2023-10-12 DOI:10.1007/s11004-023-10104-7

Peter A. Dowd, Eulogio Pardo-Igúzquiza

{"title":"协同克里格的多种形式:多元空间估计量的多样性","authors":"Peter A. Dowd, Eulogio Pardo-Igúzquiza","doi":"10.1007/s11004-023-10104-7","DOIUrl":null,"url":null,"abstract":"Abstract In this expository review paper, we show that co-kriging, a widely used geostatistical multivariate optimal linear estimator, has a diverse range of extensions that we have collected and illustrated to show the potential of this spatial interpolator. In the context of spatial stochastic processes, this paper covers scenarios including increasing the spatial resolution of a spatial variable (downscaling), solving inverse problems, estimating directional derivatives, and spatial interpolation taking boundary conditions into account. All these spatial interpolators are optimal linear estimators in the sense of being unbiased and minimising the variance of the estimation error.","PeriodicalId":51117,"journal":{"name":"Mathematical Geosciences","volume":"43 1","pages":"0"},"PeriodicalIF":2.8000,"publicationDate":"2023-10-12","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"The Many Forms of Co-kriging: A Diversity of Multivariate Spatial Estimators\",\"authors\":\"Peter A. Dowd, Eulogio Pardo-Igúzquiza\",\"doi\":\"10.1007/s11004-023-10104-7\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"Abstract In this expository review paper, we show that co-kriging, a widely used geostatistical multivariate optimal linear estimator, has a diverse range of extensions that we have collected and illustrated to show the potential of this spatial interpolator. In the context of spatial stochastic processes, this paper covers scenarios including increasing the spatial resolution of a spatial variable (downscaling), solving inverse problems, estimating directional derivatives, and spatial interpolation taking boundary conditions into account. All these spatial interpolators are optimal linear estimators in the sense of being unbiased and minimising the variance of the estimation error.\",\"PeriodicalId\":51117,\"journal\":{\"name\":\"Mathematical Geosciences\",\"volume\":\"43 1\",\"pages\":\"0\"},\"PeriodicalIF\":2.8000,\"publicationDate\":\"2023-10-12\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Mathematical Geosciences\",\"FirstCategoryId\":\"1085\",\"ListUrlMain\":\"https://doi.org/10.1007/s11004-023-10104-7\",\"RegionNum\":3,\"RegionCategory\":\"地球科学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"GEOSCIENCES, MULTIDISCIPLINARY\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Mathematical Geosciences","FirstCategoryId":"1085","ListUrlMain":"https://doi.org/10.1007/s11004-023-10104-7","RegionNum":3,"RegionCategory":"地球科学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"GEOSCIENCES, MULTIDISCIPLINARY","Score":null,"Total":0}

引用次数: 0

摘要

在这篇解释性的综述文章中，我们展示了共同克里格，一个广泛使用的地统计多元最优线性估计，我们收集并说明了这个空间插值器的潜力，并有不同的扩展范围。在空间随机过程的背景下，本文涵盖的场景包括增加空间变量的空间分辨率(降尺度)、求解逆问题、估计方向导数以及考虑边界条件的空间插值。所有这些空间插值器在无偏性和最小化估计误差方差的意义上都是最优线性估计器。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

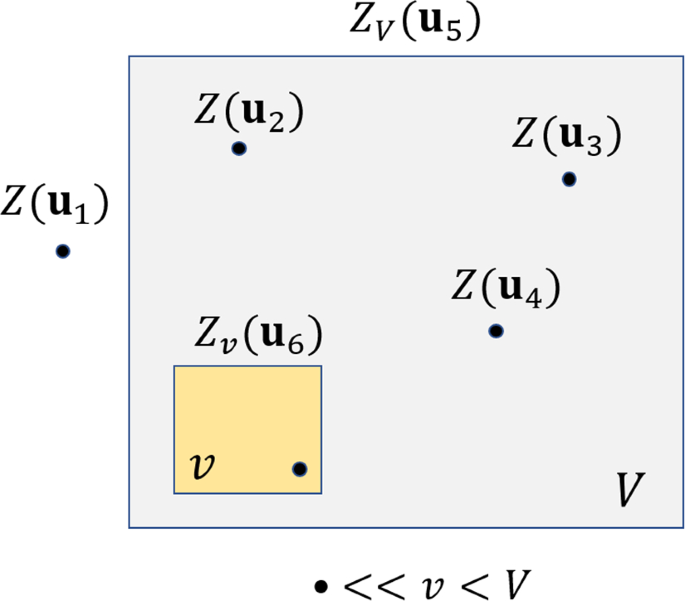
The Many Forms of Co-kriging: A Diversity of Multivariate Spatial Estimators

查看原文本刊更多论文

The Many Forms of Co-kriging: A Diversity of Multivariate Spatial Estimators

Abstract In this expository review paper, we show that co-kriging, a widely used geostatistical multivariate optimal linear estimator, has a diverse range of extensions that we have collected and illustrated to show the potential of this spatial interpolator. In the context of spatial stochastic processes, this paper covers scenarios including increasing the spatial resolution of a spatial variable (downscaling), solving inverse problems, estimating directional derivatives, and spatial interpolation taking boundary conditions into account. All these spatial interpolators are optimal linear estimators in the sense of being unbiased and minimising the variance of the estimation error.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Mathematical Geosciences 地学-地球科学综合

CiteScore

5.30

自引率

15.40%

发文量

审稿时长

>12 weeks

期刊介绍： Mathematical Geosciences (formerly Mathematical Geology) publishes original, high-quality, interdisciplinary papers in geomathematics focusing on quantitative methods and studies of the Earth, its natural resources and the environment. This international publication is the official journal of the IAMG. Mathematical Geosciences is an essential reference for researchers and practitioners of geomathematics who develop and apply quantitative models to earth science and geo-engineering problems.