具有交叉扩散的可激FitzHugh-Nagumo模型:远程激活不稳定性
IF 1.1
4区 数学
Q1 MATHEMATICS
引用次数: 0
摘要
在本文中,我们将研究FitzHugh-Nagumo模型的空间扩展版本,其中描述了物种通过交叉扩散的运动。动机来自于对相互作用影响空间运动的生物物种的建模。我们将集中分析该系统的可激态。在这种情况下,我们将看到交叉扩散项如何破坏均匀平衡,从而形成接近平衡的模式;物种在空间上呈非相分布,即一种物种的高集中区对应另一种物种的低密度(交叉图灵模式)。此外,根据抑制剂交叉扩散的大小,在抑制剂/活化剂扩散比大于或小于1的情况下,模式的发展都可以进行。这允许在短程激活/远程抑制或远程激活/短程抑制两种情况下物种的空间隔离。本文章由计算机程序翻译,如有差异,请以英文原文为准。
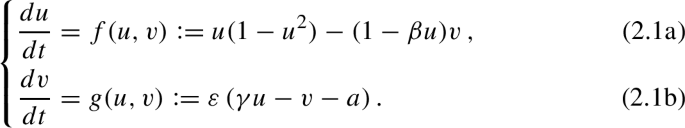
Excitable FitzHugh-Nagumo model with cross-diffusion: long-range activation instabilities
Abstract In this paper, we shall study a spatially extended version of the FitzHugh-Nagumo model, where one describes the motion of the species through cross-diffusion. The motivation comes from modeling biological species where reciprocal interaction influences spatial movement. We shall focus our analysis on the excitable regime of the system. In this case, we shall see how cross-diffusion terms can destabilize uniform equilibrium, allowing for the formation of close-to-equilibrium patterns; the species are out-of-phase spatially distributed, namely high concentration areas of one species correspond to a low density of the other (cross-Turing patterns). Moreover, depending on the magnitude of the inhibitor’s cross-diffusion, the pattern’s development can proceed in either case of the inhibitor/activator diffusivity ratio being higher or smaller than unity. This allows for spatial segregation of the species in both cases of short-range activation/long-range inhibition or long-range activation/short-range inhibition.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Ricerche di Matematica
Mathematics-Applied Mathematics
CiteScore
3.00
自引率
8.30%
发文量
61
期刊介绍:
“Ricerche di Matematica” publishes high-quality research articles in any field of pure and applied mathematics. Articles must be original and written in English. Details about article submission can be found online.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


