流动系统的时空不稳定性:比较
IF 1.1
4区 数学
Q1 MATHEMATICS
引用次数: 0
摘要
摘要对流动系统中时间不稳定和空间不稳定的定义进行了比较研究。一维Burgers流的简单模型被作为描述这些不同不稳定性概念的场景。不稳定性的时间分析源于李亚普诺夫的理论,而不稳定性的空间分析在定义演化变量时互换了时间和空间。因此,当坐标作为演化变量时,将基本流态的时间不稳定扰动的增长率参数替换为空间增长率。最后,将空间不稳定性的思想应用于具有各向异性渗透率和不渗透边界保持在不同均匀温度的饱和流体水平多孔层所给出的rayleigh - b本文章由计算机程序翻译,如有差异,请以英文原文为准。
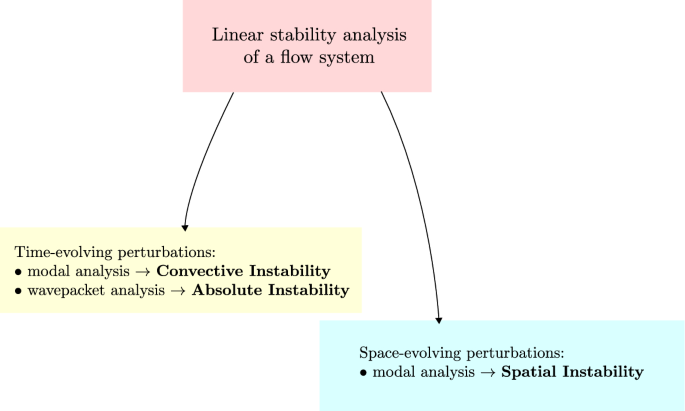
Temporal to spatial instability in a flow system: a comparison
Abstract The definitions of temporal instability and of spatial instability in a flow system are comparatively surveyed. The simple model of one-dimensional Burgers’ flow is taken as the scenario where such different conceptions of instability are described. The temporal analysis of instability stems from Lyapunov’s theory, while the spatial analysis of instability interchanges time and space in defining the evolution variable. Thus, the growth rate parameter for temporally unstable perturbations of a basic flow state is to be replaced by a spatial growth rate when a coordinate assumes the role of evolution variable. Finally, the idea of spatial instability is applied to a Rayleigh-Bénard system given by a fluid-saturated horizontal porous layer with an anisotropic permeability and impermeable boundaries kept at different uniform temperatures.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Ricerche di Matematica
Mathematics-Applied Mathematics
CiteScore
3.00
自引率
8.30%
发文量
61
期刊介绍:
“Ricerche di Matematica” publishes high-quality research articles in any field of pure and applied mathematics. Articles must be original and written in English. Details about article submission can be found online.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


