五年级STEM活动中的插值和外推:在没有高级统计的情况下探索粘度数据
IF 1.3
Q3 EDUCATION, SCIENTIFIC DISCIPLINES
引用次数: 1
摘要
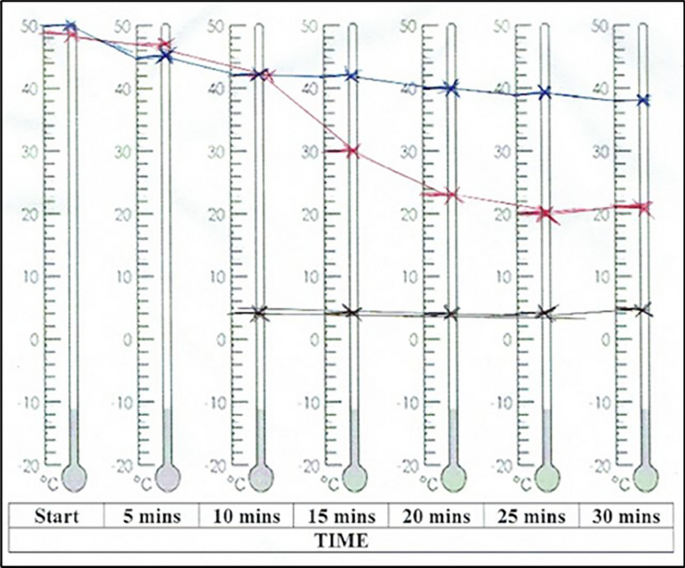
在STEM教育中采用基于证据的方法,在学习科学概念时使用数据收集和分析策略,可以增强小学生的学科知识和认知发展。本文报告了一些学习活动,这些活动利用粘度的性质和非正式统计推断的力量来建立学生对插值和外推的概念理解,而不要求他们理解用于探索第三层次概念的非线性数学。采用探索性研究策略来调查五年级学生在进行粘度实验时收集的数据创建和分析图形表示的方式。学生产生的数据表示及其随后的预测使用观察学习成果结构(SOLO)模型进行分析,该模型专门用于图形表示。结果表明,当提供适当的技术工具来支持学生的学习时,在这种情况下,TinkerPlots™,学生在STEM课程中有意义的数据背景下对插值和外推的欣赏的发展不必等到高等教育水平。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Interpolation and extrapolation in Year 5 STEM activities: exploring data about viscosity without advanced statistics
Abstract Incorporating an evidence-based approach in STEM education using data collection and analysis strategies when learning about science concepts enhances primary students’ discipline knowledge and cognitive development. This paper reports on learning activities that use the nature of viscosity and the power of informal statistical inference to build students’ conceptual understanding of interpolation and extrapolation without imposing on them the demands of understanding the nonlinear mathematics used to explore the concepts at the tertiary level. An exploratory research strategy was adopted to investigate the way in which Year 5 students created and analysed graphical representations from data collected when performing viscosity experiments. The data representations produced by the students and their subsequent predictions were analysed using the Structure of Observed Learning Outcomes (SOLO) model as adapted specifically for graphical representations. The results illustrate that when provided with appropriate technological tools to scaffold student learning, in this case TinkerPlots ™, development of students’ appreciation of interpolation and extrapolation within meaningful data contexts across the STEM curriculum does not have to wait until the tertiary level.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Mathematics Education Research Journal
EDUCATION, SCIENTIFIC DISCIPLINES-
CiteScore
4.80
自引率
11.10%
发文量
30
期刊介绍:
The Mathematics Education Research Journal seeks to promote high quality research that is of interest to the international community. The Mathematics Education Research Journal seeks to present research that promotes new knowledge, ideas, methodologies and epistemologies in the field of mathematics education. The Mathematics Education Research Journal actively seeks to promote research from the Australasian region either as research conducted in the region; conducted by researchers from the region and/or draws on research from the region. The Mathematics Education Research Journal accepts papers from authors from all regions internationally but authors must draw on the extensive research that has been produced in the Australasian region. The Mathematics Education Research Journal normally does not encourage publication of teacher education programs or courses. These are more suited for theother MERGA journal, Mathematics Teacher Education and Development.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


