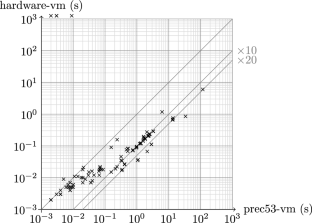
Enabling Floating-Point Arithmetic in the Coq Proof Assistant

Floating-point arithmetic is a well-known and extremely efficient way of performing approximate computations over the real numbers. Although it requires some careful considerations, floating-point numbers are nowadays routinely used to prove mathematical theorems. Numerical computations have been applied in the context of formal proofs too, as illustrated by the CoqInterval library. But these computations do not benefit from the powerful floating-point units available in modern processors, since they are emulated inside the logic of the formal system. This paper experiments with the use of hardware floating-point numbers for numerically intensive proofs verified by the Coq proof assistant. This gives rise to various questions regarding the formalization, the implementation, the usability, and the level of trust. This approach has been applied to the CoqInterval and ValidSDP libraries, which demonstrates a speedup of at least one order of magnitude.