Worst-Case Optimal Covering of Rectangles by Disks

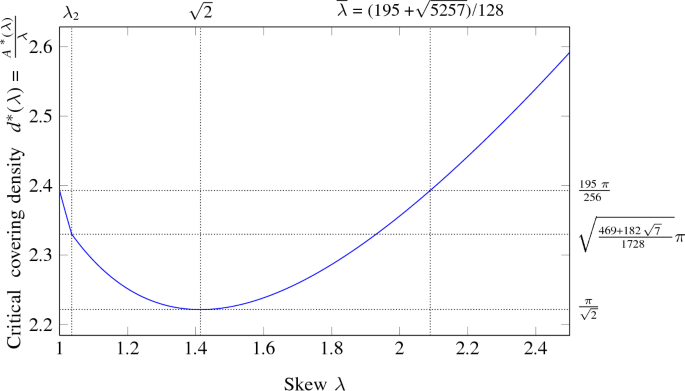
Abstract We provide the solution for a fundamental problem of geometric optimization by giving a complete characterization of worst-case optimal disk coverings of rectangles: For any $$\lambda \ge 1$$ λ ≥ 1 , the critical covering area $$A^*(\lambda )$$ A ∗ ( λ ) is the minimum value for which any set of disks with total area at least $$A^*(\lambda )$$ A ∗ ( λ ) can cover a rectangle of dimensions $$\lambda \times 1$$ λ × 1 . We show that there is a threshold value $$\lambda _2 = \sqrt{\sqrt{7}/2 - 1/4} \approx 1.035797\ldots $$ λ 2 = 7 / 2 - 1 / 4 ≈ 1.035797 … , such that for $$\lambda <\lambda _2$$ λ < λ 2 the critical covering area $$A^*(\lambda )$$ A ∗ ( λ ) is $$A^*(\lambda )=3\pi \left( \frac{\lambda ^2}{16} +\frac{5}{32} + \frac{9}{256\lambda ^2}\right) $$ A ∗ ( λ ) = 3 π λ 2 16 + 5 32 + 9 256 λ 2 , and for $$\lambda \ge \lambda _2$$ λ ≥ λ 2 , the critical area is $$A^*(\lambda )=\pi (\lambda ^2+2)/4$$ A ∗ ( λ ) = π ( λ 2 + 2 ) / 4 ; these values are tight. For the special case $$\lambda =1$$ λ = 1 , i.e., for covering a unit square, the critical covering area is $$\frac{195\pi }{256}\approx 2.39301\ldots $$ 195 π 256 ≈ 2.39301 … . The proof uses a careful combination of manual and automatic analysis, demonstrating the power of the employed interval arithmetic technique.