用欧拉方法研究有限应变粘弹性多极固体与流体的相互作用

IF 1.2 3区数学 Q2 MATHEMATICS, APPLIED

Journal of Mathematical Fluid Mechanics Pub Date : 2023-09-23 DOI:10.1007/s00021-023-00817-4

Tomáš Roubíček

{"title":"用欧拉方法研究有限应变粘弹性多极固体与流体的相互作用","authors":"Tomáš Roubíček","doi":"10.1007/s00021-023-00817-4","DOIUrl":null,"url":null,"abstract":"<div><p>A mechanical interaction of compressible viscoelastic fluids with viscoelastic solids in Kelvin–Voigt rheology using the concept of higher-order (so-called 2nd-grade multipolar) viscosity is investigated in a quasistatic variant. The no-slip contact between fluid and solid is considered and the Eulerian-frame return-mapping technique is used for both the fluid and the solid models, which allows for a “monolithic” formulation of this fluid–structure interaction problem. Existence and a certain regularity of weak solutions is proved by a Schauder fixed-point argument combined with a suitable regularization.</p></div>","PeriodicalId":649,"journal":{"name":"Journal of Mathematical Fluid Mechanics","volume":"25 4","pages":""},"PeriodicalIF":1.2000,"publicationDate":"2023-09-23","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"1","resultStr":"{\"title\":\"Interaction of Finitely-Strained Viscoelastic Multipolar Solids and Fluids by an Eulerian Approach\",\"authors\":\"Tomáš Roubíček\",\"doi\":\"10.1007/s00021-023-00817-4\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div><p>A mechanical interaction of compressible viscoelastic fluids with viscoelastic solids in Kelvin–Voigt rheology using the concept of higher-order (so-called 2nd-grade multipolar) viscosity is investigated in a quasistatic variant. The no-slip contact between fluid and solid is considered and the Eulerian-frame return-mapping technique is used for both the fluid and the solid models, which allows for a “monolithic” formulation of this fluid–structure interaction problem. Existence and a certain regularity of weak solutions is proved by a Schauder fixed-point argument combined with a suitable regularization.</p></div>\",\"PeriodicalId\":649,\"journal\":{\"name\":\"Journal of Mathematical Fluid Mechanics\",\"volume\":\"25 4\",\"pages\":\"\"},\"PeriodicalIF\":1.2000,\"publicationDate\":\"2023-09-23\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"1\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of Mathematical Fluid Mechanics\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s00021-023-00817-4\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"MATHEMATICS, APPLIED\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Mathematical Fluid Mechanics","FirstCategoryId":"100","ListUrlMain":"https://link.springer.com/article/10.1007/s00021-023-00817-4","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"MATHEMATICS, APPLIED","Score":null,"Total":0}

引用次数: 1

摘要

利用高阶(所谓的二级多极)粘度的概念，在准静态变量中研究了可压缩粘弹性流体与粘弹性固体在Kelvin-Voigt流变中的力学相互作用。考虑了流体和固体之间的无滑移接触，并将欧拉框架返回映射技术用于流体和固体模型，从而允许对该流固相互作用问题进行“整体”表述。利用Schauder不动点论证结合适当的正则化证明了弱解的存在性和一定的正则性。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

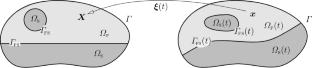
Interaction of Finitely-Strained Viscoelastic Multipolar Solids and Fluids by an Eulerian Approach

查看原文本刊更多论文

Interaction of Finitely-Strained Viscoelastic Multipolar Solids and Fluids by an Eulerian Approach

A mechanical interaction of compressible viscoelastic fluids with viscoelastic solids in Kelvin–Voigt rheology using the concept of higher-order (so-called 2nd-grade multipolar) viscosity is investigated in a quasistatic variant. The no-slip contact between fluid and solid is considered and the Eulerian-frame return-mapping technique is used for both the fluid and the solid models, which allows for a “monolithic” formulation of this fluid–structure interaction problem. Existence and a certain regularity of weak solutions is proved by a Schauder fixed-point argument combined with a suitable regularization.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of Mathematical Fluid Mechanics 物理-力学

CiteScore

2.00

自引率

15.40%

发文量

审稿时长

>12 weeks

期刊介绍： The Journal of Mathematical Fluid Mechanics (JMFM)is a forum for the publication of high-quality peer-reviewed papers on the mathematical theory of fluid mechanics, with special regards to the Navier-Stokes equations. As an important part of that, the journal encourages papers dealing with mathematical aspects of computational theory, as well as with applications in science and engineering. The journal also publishes in related areas of mathematics that have a direct bearing on the mathematical theory of fluid mechanics. All papers will be characterized by originality and mathematical rigor. For a paper to be accepted, it is not enough that it contains original results. In fact, results should be highly relevant to the mathematical theory of fluid mechanics, and meet a wide readership.