Zero-Temperature Stochastic Ising Model on Planar Quasi-Transitive Graphs
IF 1.2
3区 物理与天体物理
Q3 PHYSICS, MATHEMATICAL
引用次数: 0
Abstract
We study the zero-temperature stochastic Ising model on some connected planar quasi-transitive graphs, which are invariant under rotations and translations. The initial spin configuration is distributed according to a Bernoulli product measure with parameter \( p\in (0,1) \). In particular, we prove that if \( p=1/2 \) and the graph underlying the model satisfies the planar shrink property then all vertices flip infinitely often almost surely.
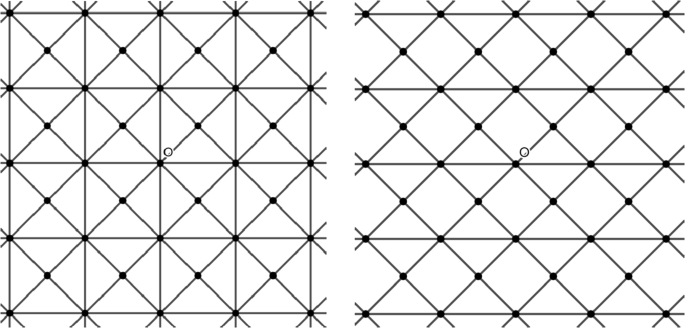
平面拟传递图上的零温度随机Ising模型
我们研究了一些连通平面拟传递图上的零温度随机Ising模型,这些图在旋转和平移下是不变的。初始自旋构型是根据参数为\(p\in(0,1)\)的伯努利乘积测度分布的。特别地,我们证明了如果\(p=1/2\)和模型下的图满足平面收缩性质,那么所有顶点几乎肯定地无限翻转。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Journal of Statistical Physics
物理-物理:数学物理
CiteScore
3.10
自引率
12.50%
发文量
152
审稿时长
3-6 weeks
期刊介绍:
The Journal of Statistical Physics publishes original and invited review papers in all areas of statistical physics as well as in related fields concerned with collective phenomena in physical systems.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


