Side-Comparison for Transition Maps in Multi-Layer Canard Problems
IF 0.8
4区 数学
Q3 MATHEMATICS, APPLIED
引用次数: 0
Abstract
The paper deals with multi-layer canard cycles, extending the results of [1]. As a practical tool we introduce the connection diagram of a canard cycle and we show how to determine it in an easy way. This connection diagram presents in a clear way all available information that is necessary to formulate the main system of equations used in the study of the bifurcating limit cycles. In a forthcoming paper we will show that both the type of the layers and the nature of the connections between the layers play an essential role in determining the number and the bifurcations of the limit cycles that can be created from a canard cycle.
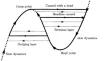
多层Canard问题中过渡映射的边比较
本文讨论了多层鸭式循环,扩展了[1]的结果。作为一个实用工具,我们介绍了鸭式循环的连接图,并展示了如何以简单的方式确定它。这个连接图以一种清晰的方式呈现了所有可用的信息,这些信息是制定用于研究分叉极限环的主要方程组所必需的。在即将发表的一篇论文中,我们将表明,层的类型和层之间连接的性质在确定可由鸭式循环产生的极限循环的数量和分叉方面发挥着重要作用。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
2.50
自引率
7.10%
发文量
35
审稿时长
>12 weeks
期刊介绍:
Regular and Chaotic Dynamics (RCD) is an international journal publishing original research papers in dynamical systems theory and its applications. Rooted in the Moscow school of mathematics and mechanics, the journal successfully combines classical problems, modern mathematical techniques and breakthroughs in the field. Regular and Chaotic Dynamics welcomes papers that establish original results, characterized by rigorous mathematical settings and proofs, and that also address practical problems. In addition to research papers, the journal publishes review articles, historical and polemical essays, and translations of works by influential scientists of past centuries, previously unavailable in English. Along with regular issues, RCD also publishes special issues devoted to particular topics and events in the world of dynamical systems.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


