Lattices of retracts of direct products of two finite chains and notes on retracts of lattices
IF 0.6
4区 数学
Q3 MATHEMATICS
引用次数: 1
Abstract
Ordered by set inclusion, the retracts of a lattice L together with the empty set form a bounded poset \(Ret (L)\). By a grid we mean the direct product of two non-singleton finite chains. We prove that if G is a grid, then \(Ret (G)\) is a lattice. We determine the number of elements of \(Ret (G)\). Some easy properties of retracts, retractions, and their kernels called retraction congruences of (mainly distributive) lattices are found. Also, we present several examples, including a 12-element modular lattice M such that \(Ret (M)\) is not a lattice.
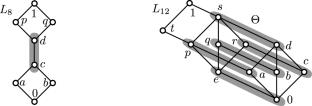
两个有限链直积的回缩格及关于回缩格的注记
按照集合包含的顺序,格L的收缩与空集一起形成有界偏序集\(Ret(L)\)。我们所说的网格是指两个非单例有限链的直积。我们证明了如果G是一个网格,那么\(Ret(G)\)是一个格。我们确定\(Ret(G)\)的元素数。发现了回缩、回缩及其核的一些简单性质,称为(主要是分配的)格的回缩同余。此外,我们给出了几个例子,包括一个12元模格M,使得\(Ret(M)\)不是格。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Algebra Universalis
数学-数学
CiteScore
1.00
自引率
16.70%
发文量
34
审稿时长
3 months
期刊介绍:
Algebra Universalis publishes papers in universal algebra, lattice theory, and related fields. In a pragmatic way, one could define the areas of interest of the journal as the union of the areas of interest of the members of the Editorial Board. In addition to research papers, we are also interested in publishing high quality survey articles.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


