Optimal Hardy-weights for elliptic operators with mixed boundary conditions

IF 0.8 3区数学 Q2 MATHEMATICS

Mathematika Pub Date : 2023-09-28 DOI:10.1112/mtk.12226

Yehuda Pinchover, Idan Versano

{"title":"Optimal Hardy-weights for elliptic operators with mixed boundary conditions","authors":"Yehuda Pinchover, Idan Versano","doi":"10.1112/mtk.12226","DOIUrl":null,"url":null,"abstract":"We construct families of optimal Hardy-weights for a subcritical linear second-order elliptic operator <math>\n <semantics>\n <mrow>\n <mo>(</mo>\n <mi>P</mi>\n <mo>,</mo>\n <mi>B</mi>\n <mo>)</mo>\n </mrow>\n <annotation>$(P,B)$</annotation>\n </semantics></math> with degenerate mixed boundary conditions. By an optimal Hardy-weight for a subcritical operator we mean a nonzero nonnegative weight function W such that <math>\n <semantics>\n <mrow>\n <mo>(</mo>\n <mi>P</mi>\n <mo>−</mo>\n <mi>W</mi>\n <mo>,</mo>\n <mi>B</mi>\n <mo>)</mo>\n </mrow>\n <annotation>$(P-W,B)$</annotation>\n </semantics></math> is critical, and null-critical with respect to W. Our results rely on a recently developed criticality theory for positive solutions of the corresponding mixed boundary value problem.","PeriodicalId":18463,"journal":{"name":"Mathematika","volume":null,"pages":null},"PeriodicalIF":0.8000,"publicationDate":"2023-09-28","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://onlinelibrary.wiley.com/doi/epdf/10.1112/mtk.12226","citationCount":"0","resultStr":null,"platform":"Semanticscholar","paperid":null,"PeriodicalName":"Mathematika","FirstCategoryId":"100","ListUrlMain":"https://onlinelibrary.wiley.com/doi/10.1112/mtk.12226","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

Abstract

We construct families of optimal Hardy-weights for a subcritical linear second-order elliptic operator $(P, B)$ with degenerate mixed boundary conditions. By an optimal Hardy-weight for a subcritical operator we mean a nonzero nonnegative weight function W such that $(P - W, B)$ is critical, and null-critical with respect to W. Our results rely on a recently developed criticality theory for positive solutions of the corresponding mixed boundary value problem.

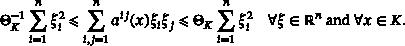
Abstract Image

查看原文本刊更多论文

混合边界条件下椭圆算子的最优Hardy权

我们构造了具有退化混合边界条件的次临界线性二阶椭圆算子（P，B）$（P，B）$的最优Hardy权族。次临界算子的最优Hardy权是指非零非负权函数W，使得（P−W，B）$（P-W，B，和关于W的零临界。我们的结果依赖于最近发展的临界理论，用于相应的混合边值问题的正解。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Mathematika MATHEMATICS, APPLIED-MATHEMATICS

CiteScore

1.40

自引率

0.00%

发文量

审稿时长

>12 weeks

期刊介绍： Mathematika publishes both pure and applied mathematical articles and has done so continuously since its founding by Harold Davenport in the 1950s. The traditional emphasis has been towards the purer side of mathematics but applied mathematics and articles addressing both aspects are equally welcome. The journal is published by the London Mathematical Society, on behalf of its owner University College London, and will continue to publish research papers of the highest mathematical quality.