Weakly Schreier extensions for general algebras

Abstract

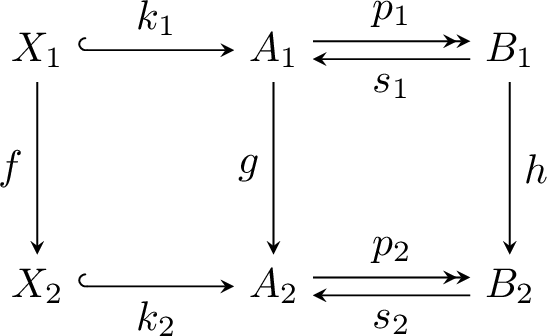
Weakly Schreier split extensions are a reasonably large, yet well-understood class of monoid extensions, which generalise some aspects of split extensions of groups. This short note provides a way to define and study similar classes of split extensions in general algebraic structures (parameterised by a term \(\theta \)). These generalise weakly Schreier extensions of monoids, as well as general extensions of semi-abelian varieties (using the \(\theta \) appearing in their syntactic characterisation). Restricting again to the case of monoids, a different choice of \(\theta \) leads to a new class of monoid extensions, more general than the weakly Schreier split extensions.