A note on the zeros of the derivatives of Hardy's function Z ( t ) $Z(t)$

Abstract

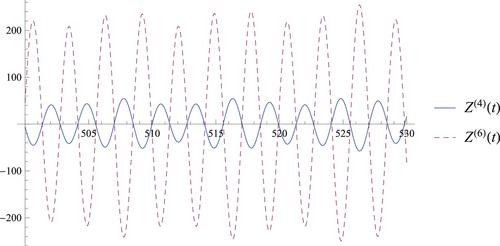
Using the twisted fourth moment of the Riemann zeta-function, we study large gaps between consecutive zeros of the derivatives of Hardy's function $Z\left(t\right)$, improving upon previous results of Conrey and Ghosh (J. Lond. Math. Soc. 32 (1985) 193–202), and of the second named author (Acta Arith. 111 (2004) 125–140). We also exhibit small distances between the zeros of $Z\left(t\right)$ and the zeros of $Z^{\left(2k\right)}\left(t\right)$ for every $k\in N$, in support of our numerical observation that the zeros of $Z^{\left(k\right)}\left(t\right)$ and $Z^{\left(\ell \right)}\left(t\right)$, when k and ℓ have the same parity, seem to come in pairs that are very close to each other. The latter result is obtained using the mollified discrete second moment of the Riemann zeta-function.