Affine subspace concentration conditions for centered polytopes

IF 0.8 3区数学 Q2 MATHEMATICS

Mathematika Pub Date : 2023-02-13 DOI:10.1112/mtk.12189

Ansgar Freyer, Martin Henk, Christian Kipp

引用次数: 2

Abstract

Recently, K.-Y. Wu introduced affine subspace concentration conditions for the cone volumes of polytopes and proved that the cone volumes of centered, reflexive, smooth lattice polytopes satisfy these conditions. We extend the result to arbitrary centered polytopes.

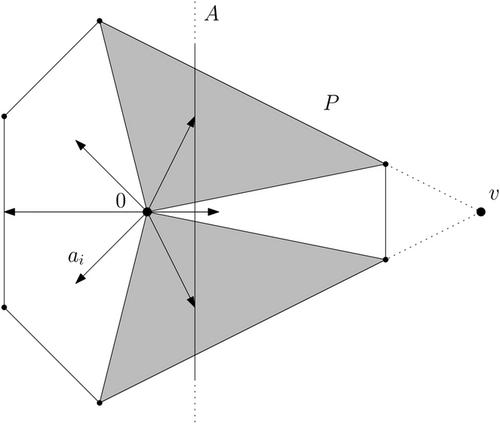
Abstract Image

查看原文本刊更多论文

中心多面体的仿射子空间集中条件

最近，吴引入了多面体锥体积的仿射子空间集中条件，并证明了中心自反光滑格多面体的锥体积满足这些条件。我们将结果推广到任意中心的多面体。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Mathematika MATHEMATICS, APPLIED-MATHEMATICS

CiteScore

1.40

自引率

0.00%

发文量

审稿时长

>12 weeks

期刊介绍： Mathematika publishes both pure and applied mathematical articles and has done so continuously since its founding by Harold Davenport in the 1950s. The traditional emphasis has been towards the purer side of mathematics but applied mathematics and articles addressing both aspects are equally welcome. The journal is published by the London Mathematical Society, on behalf of its owner University College London, and will continue to publish research papers of the highest mathematical quality.