Affine Geometry and Relativity

IF 1.2 3区物理与天体物理 Q3 PHYSICS, MULTIDISCIPLINARY

Foundations of Physics Pub Date : 2023-06-05 DOI:10.1007/s10701-023-00700-2

Božidar Jovanović

引用次数: 0

Abstract

We present the basic concepts of space and time, the Galilean and pseudo-Euclidean geometry. We use an elementary geometric framework of affine spaces and groups of affine transformations to illustrate the natural relationship between classical mechanics and theory of relativity, which is quite often hidden, despite its fundamental importance. We have emphasized a passage from the group of Galilean motions to the group of Poincaré transformations of a plane. In particular, a 1-parametric family of natural deformations of the Poincaré group is described. We also visualized the underlying groups of Galilean, Euclidean, and pseudo-Euclidean rotations within the special linear group.

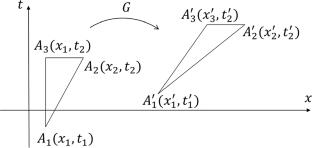
Abstract Image

查看原文本刊更多论文

仿射几何与相对论

我们提出了空间和时间的基本概念，伽利略和伪欧几里得几何。我们使用仿射空间和仿射变换群的基本几何框架来说明经典力学和相对论之间的自然关系，尽管它具有基本的重要性，但这种关系往往是隐藏的。我们已经强调了从伽利略运动群到庞加莱变换群的过渡。特别地，描述了庞卡洛群的自然变形的1参数族。我们还可视化了特殊线性群内的伽利略、欧几里得和伪欧几里得旋转的基础群。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Foundations of Physics 物理-物理：综合

CiteScore

2.70

自引率

6.70%

发文量

104

审稿时长

6-12 weeks

期刊介绍： The conceptual foundations of physics have been under constant revision from the outset, and remain so today. Discussion of foundational issues has always been a major source of progress in science, on a par with empirical knowledge and mathematics. Examples include the debates on the nature of space and time involving Newton and later Einstein; on the nature of heat and of energy; on irreversibility and probability due to Boltzmann; on the nature of matter and observation measurement during the early days of quantum theory; on the meaning of renormalisation, and many others. Today, insightful reflection on the conceptual structure utilised in our efforts to understand the physical world is of particular value, given the serious unsolved problems that are likely to demand, once again, modifications of the grammar of our scientific description of the physical world. The quantum properties of gravity, the nature of measurement in quantum mechanics, the primary source of irreversibility, the role of information in physics – all these are examples of questions about which science is still confused and whose solution may well demand more than skilled mathematics and new experiments. Foundations of Physics is a privileged forum for discussing such foundational issues, open to physicists, cosmologists, philosophers and mathematicians. It is devoted to the conceptual bases of the fundamental theories of physics and cosmology, to their logical, methodological, and philosophical premises. The journal welcomes papers on issues such as the foundations of special and general relativity, quantum theory, classical and quantum field theory, quantum gravity, unified theories, thermodynamics, statistical mechanics, cosmology, and similar.