System of sequences in multivariate reticular structures
IF 79.8
1区 材料科学
Q1 MATERIALS SCIENCE, MULTIDISCIPLINARY
引用次数: 16
Abstract
When variance is encountered in reticular structures such as metal–organic frameworks, it occurs as multiple kinds of functionalities bound and distributed in aperiodic lattices. In these multivariate systems, unknown spatial arrangements of functionalities create properties that go beyond those of their simple sum. It is therefore essential that we learn how to recognize, study and use these arrangements, and for this purpose we propose using the concept of sequences. Accordingly, we propose a classification system, outline a method for characterizing sequences and describe the application to self-propelled reticular machines. On a fundamental level, this contribution transforms the chemist’s thinking from the usual ‘make, characterize, use’ protocol of doing chemistry to a discovery routine based on finding correlations between input synthesis parameters and output performance. This approach provides an alternative and widely accessible pathway for determining the properties that the system of sequences confers on multivariate reticular structures. One of the most advanced and challenging topics in modern reticular chemistry is structure multivariation. This Perspective defines the fundamentals of multivariation by considering sequences of chemical species as its true essence, thereby addressing the classification of multivariate structures and presenting new concepts for their analysis and application.
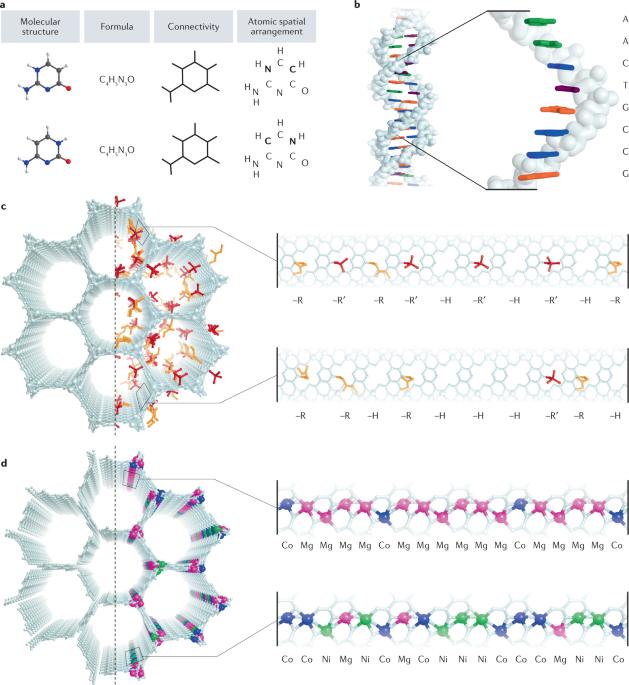
多元网状结构中的序列系统
当网状结构(如金属有机框架)中出现差异时,它是由多种功能结合并分布在非周期性晶格中产生的。在这些多变量系统中,未知的功能空间排列会产生超越其简单总和的特性。因此,我们必须学会如何识别、研究和使用这些排列,为此,我们建议使用序列的概念。因此,我们提出了一个分类系统,概述了描述序列特征的方法,并描述了在自走式网状机器中的应用。从根本上说,这一贡献将化学家的思维从通常的 "制造、表征、使用 "化学方法转变为基于寻找输入合成参数与输出性能之间相关性的发现程序。这种方法为确定序列系统赋予多变量网状结构的特性提供了另一种可广泛利用的途径。结构多变量是现代网状结构化学中最先进、最具挑战性的课题之一。本视角将化学物种序列视为多元结构的真正本质,从而定义了多元结构的基本原理,解决了多元结构的分类问题,并提出了分析和应用多元结构的新概念。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Nature Reviews Materials
Materials Science-Biomaterials
CiteScore
119.40
自引率
0.40%
发文量
107
期刊介绍:
Nature Reviews Materials is an online-only journal that is published weekly. It covers a wide range of scientific disciplines within materials science. The journal includes Reviews, Perspectives, and Comments.
Nature Reviews Materials focuses on various aspects of materials science, including the making, measuring, modelling, and manufacturing of materials. It examines the entire process of materials science, from laboratory discovery to the development of functional devices.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


