A concise proof of Benford’s law
IF 6.2
3区 综合性期刊
Q1 Multidisciplinary
引用次数: 0
Abstract
This article presents a concise proof of the famous Benford’s law when the distribution has a Riemann integrable probability density function and provides a criterion to judge whether a distribution obeys the law. The proof is intuitive and elegant, accessible to anyone with basic knowledge of calculus, revealing that the law originates from the basic property of human number system. The criterion can bring great convenience to the field of fraud detection.
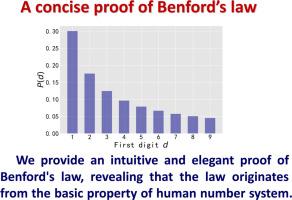
Benford定律的简明证明
本文简明扼要地证明了当分布具有黎曼可积分概率密度函数时的著名本福德定律,并提供了判断分布是否服从该定律的标准。证明直观而优雅,任何具有微积分基础知识的人都能理解,揭示了该定律源于人类数制的基本属性。该标准可为欺诈检测领域带来极大的便利。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Fundamental Research
Multidisciplinary-Multidisciplinary
CiteScore
4.00
自引率
1.60%
发文量
294
审稿时长
79 days
期刊介绍:
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


