The Epistemology of a Positive SARS-CoV-2 Test
Abstract
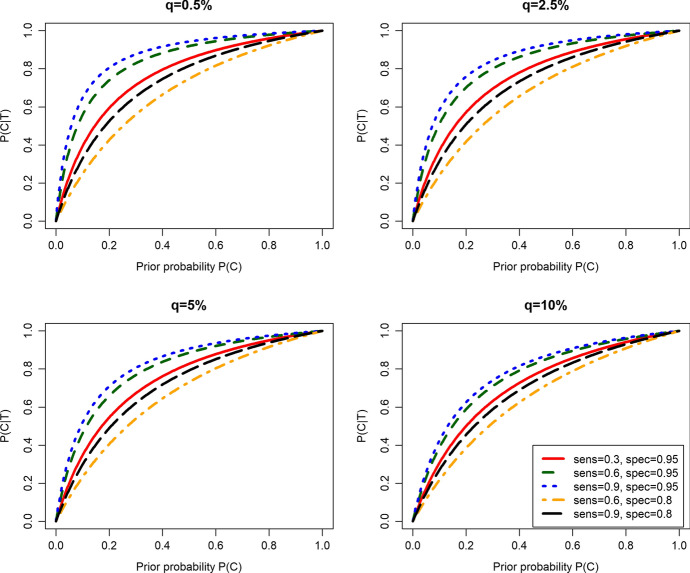
We investigate the epistemological consequences of a positive polymerase chain reaction SARS-CoV test for two relevant hypotheses: (i) V is the hypothesis that an individual has been infected with SARS-CoV-2; (ii) C is the hypothesis that SARS-CoV-2 is the cause of flu-like symptoms in a given patient. We ask two fundamental epistemological questions regarding each hypothesis: First, how much confirmation does a positive test lend to each hypothesis? Second, how much evidence does a positive test provide for each hypothesis against its negation? We respond to each question within a formal Bayesian framework. We construe degree of confirmation as the difference between the posterior probability of the hypothesis and its prior, and the strength of evidence for a hypothesis against its alternative in terms of their likelihood ratio. We find that test specificity—and coinfection probabilities when making inferences about C—were key determinants of confirmation and evidence. Tests with < 87% specificity could not provide strong evidence (likelihood ratio > 8) for V against ¬V regardless of sensitivity. Accordingly, low specificity tests could not provide strong evidence in favor of C in all plausible scenarios modeled. We also show how a positive influenza A test disconfirms C and provides weak evidence against C in dependence on the probability that the patient is influenza A infected given that his/her symptoms are not caused by SARS-CoV-2. Our analysis points out some caveats that should be considered when attributing symptoms or death of a positively tested patient to SARS-CoV-2.



 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


