Path integral methods for stochastic differential equations.

IF 2.3 4区医学 Q1 Neuroscience

Journal of Mathematical Neuroscience Pub Date : 2015-03-24 eCollection Date: 2015-01-01 DOI:10.1186/s13408-015-0018-5

Carson C Chow, Michael A Buice

引用次数: 10

Abstract

Stochastic differential equations (SDEs) have multiple applications in mathematical neuroscience and are notoriously difficult. Here, we give a self-contained pedagogical review of perturbative field theoretic and path integral methods to calculate moments of the probability density function of SDEs. The methods can be extended to high dimensional systems such as networks of coupled neurons and even deterministic systems with quenched disorder.

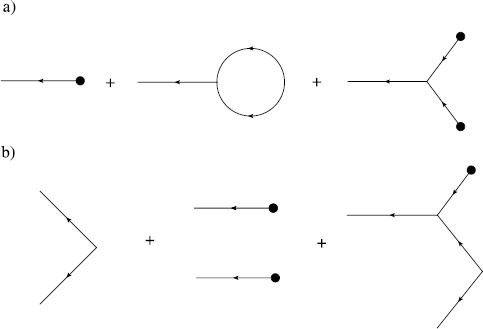
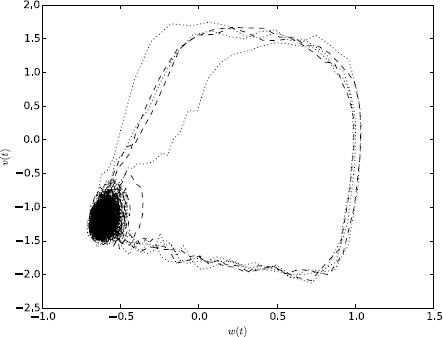
Abstract Image

查看原文本刊更多论文

随机微分方程的路径积分方法。

随机微分方程(SDEs)在数学神经科学中有多种应用，并且非常困难。在这里，我们给出了一个独立的教学回顾微扰场论和路径积分方法计算的概率密度函数的矩。该方法可以推广到高维系统，如耦合神经元网络，甚至具有淬灭无序的确定性系统。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Journal of Mathematical Neuroscience Neuroscience-Neuroscience (miscellaneous)

自引率

0.00%

发文量

审稿时长

13 weeks

期刊介绍： The Journal of Mathematical Neuroscience (JMN) publishes research articles on the mathematical modeling and analysis of all areas of neuroscience, i.e., the study of the nervous system and its dysfunctions. The focus is on using mathematics as the primary tool for elucidating the fundamental mechanisms responsible for experimentally observed behaviours in neuroscience at all relevant scales, from the molecular world to that of cognition. The aim is to publish work that uses advanced mathematical techniques to illuminate these questions. It publishes full length original papers, rapid communications and review articles. Papers that combine theoretical results supported by convincing numerical experiments are especially encouraged. Papers that introduce and help develop those new pieces of mathematical theory which are likely to be relevant to future studies of the nervous system in general and the human brain in particular are also welcome.