A linear failure index for the Christensen criterion
IF 3.8
3区 工程技术
Q1 MECHANICS
International Journal of Solids and Structures
Pub Date : 2025-10-03
DOI:10.1016/j.ijsolstr.2025.113685
引用次数: 0
Abstract
The Christensen failure criterion is a stress-based two-parameter failure criterion with two subcriteria for isotropic non-porous materials ranging from ductile materials like mild steel over plastics and cast iron to fully brittle materials like concrete or rocks. Despite reported experimental validation and wide applicability, the Christensen failure criterion is not widely used due to its complexity (combination of two subcriteria) and the lack of available implementations, e.g. in finite element software. In this work we propose a linear failure index for the Christensen criterion, akin to failure indices for fiber-reinforced plastic. The failure index is derived by projecting the stress state in spherical coordinates onto the failure surface, enabling a closed-form solution applicable also to other multi-parameter failure criteria. Additionally, the ductility number defined in the Christensen theory, describing the failure mode is implemented in the given framework. The methodology is further implemented in a new python package Christensen_FailureIndex as well as for the commercial finite element software Simulia ABAQUS (via a UMAT subroutine and also via a postprocessing Python GUI plugin) allowing for versatile use of the criterion. To assess efficiency and discuss its utility, the derived failure index is applied to a three point bending test with a notched specimen for a mildly brittle plastic to discuss critical load and failure location. The code for all implementations is publicly available on https://github.com/cld-rostock/Christensen_FailureIndex.
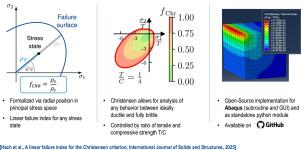
Christensen准则的线性失效指标
Christensen破坏准则是一种基于应力的双参数破坏准则,它有两个子准则,适用于各向同性无孔材料,从韧性材料(如低碳钢、塑料和铸铁)到完全脆性材料(如混凝土或岩石)。尽管报道了实验验证和广泛的适用性,Christensen失效准则并没有被广泛使用,因为它的复杂性(两个子标准的组合)和缺乏可用的实现,例如在有限元软件中。在这项工作中,我们提出了Christensen准则的线性破坏指数,类似于纤维增强塑料的破坏指数。通过将应力状态以球坐标投影到破坏面上,推导出破坏指数,得到的封闭解也适用于其他多参数破坏准则。此外,在给定的框架中实现了Christensen理论中定义的描述破坏模式的延性数。该方法在新的python包Christensen_FailureIndex以及商业有限元软件Simulia ABAQUS(通过UMAT子程序和后处理python GUI插件)中进一步实现,允许通用使用该标准。为了评估效率并讨论其实用性,将导出的破坏指数应用于轻度脆性塑料的缺口试件三点弯曲试验,以讨论临界载荷和破坏位置。所有实现的代码都可以在https://github.com/cld-rostock/Christensen_FailureIndex上公开获得。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
6.70
自引率
8.30%
发文量
405
审稿时长
70 days
期刊介绍:
The International Journal of Solids and Structures has as its objective the publication and dissemination of original research in Mechanics of Solids and Structures as a field of Applied Science and Engineering. It fosters thus the exchange of ideas among workers in different parts of the world and also among workers who emphasize different aspects of the foundations and applications of the field.
Standing as it does at the cross-roads of Materials Science, Life Sciences, Mathematics, Physics and Engineering Design, the Mechanics of Solids and Structures is experiencing considerable growth as a result of recent technological advances. The Journal, by providing an international medium of communication, is encouraging this growth and is encompassing all aspects of the field from the more classical problems of structural analysis to mechanics of solids continually interacting with other media and including fracture, flow, wave propagation, heat transfer, thermal effects in solids, optimum design methods, model analysis, structural topology and numerical techniques. Interest extends to both inorganic and organic solids and structures.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


