Bifurcation analysis using modified stiffness method of group theoretic imperfections

Abstract

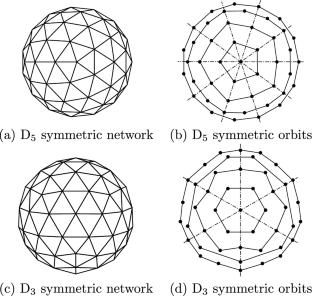
Multiple bifurcations due to symmetry often occur when analyzing nonlinear structural motifs with axial symmetry. The identification of multiple bifurcation points and the tracing of bifurcation paths become significant challenges in numerical analysis. In this paper, we address a numerical problem of nonlinear bifurcation in a symmetric structure exhibiting double bifurcation points. By focusing on the initial imperfection vector corresponding to the partial irreducible representation of its symmetry, we propose a modified stiffness method. This method utilizes the orthogonalization transformation differences to separate the multiple bifurcation points of the second-order irreducible representation of the stiffness matrix into a single bifurcation point. As a numerical example, bifurcation analysis of an axially symmetric fullerene truss structure is conducted to demonstrate the effectiveness of the proposed method. This study successfully addresses the issue of multiple bifurcations in axially symmetric structures by incorporating group-theoretic bifurcation theory and modifying the stiffness method, as validated by the numerical analysis of a fullerene truss structure.