A non-intrusive data-driven approach towards a solution of the inverse problem of bending dielectric elastomer actuators

Abstract

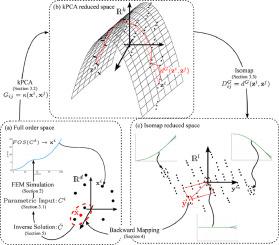
Dielectric Elastomer Actuators (DEAs), particularly bending DEAs, have gained significant attention due to their applications in soft robotics, biomimetic systems, and adaptive structures. Recent advancements in computational mechanics and the finite element method (FEM) have enabled accurate simulations of these actuators by incorporating their nonlinear mechanical behavior at large deformations and the coupling between mechanical and electrical responses. However, DEA design often involves solving inverse problems, which become computationally expensive when relying solely on direct simulations. To mitigate this cost, a fast surrogate model is needed. This study proposes a Reduced Order Model (ROM)-based methodology to efficiently determine the optimal locations and magnitudes of applied external potentials in a bending DEA to achieve a desired displacement response. The approach leverages nonlinear dimensionality reduction techniques, specifically Kernel Principal Component Analysis (kPCA) and Isometric Mapping (Isomap), to construct a surrogate model that accurately predicts DEA displacement responses from existing data without modifying the underlying FEM formulation. Using this surrogate model, the inverse problem is solved efficiently, achieving high accuracy (<2 % error) while significantly reducing computational cost. The methodology is validated on two different bending DEA geometries, demonstrating its effectiveness in both surrogate modeling and time-efficient inverse problem solving.