Inverting g(r) to u(r): The test-particle insertion method

Abstract

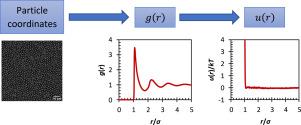
Inverting the radial distribution function, $g\left(r\right)$, to a pair potential, $u\left(r\right)$, can be achieved by a variety of methods. Test-particle insertion has recently emerged as an efficient inverse method for finding $u\left(r\right)$. The method can analyse both simulated and experimental data, and the only input required is equilibrium snapshots of particle coordinates. This paper explains the method in detail and its implementation, sharing example code. We demonstrate intricacies in the number and placement of test particles and their effect on efficiency, as well as practical advice for applying the method to experimental data. This includes strategies and code for dealing with non-periodic boundary conditions, choice of inversion cutoff distance and the effect of particles sticking. We also discuss how the method performs at higher density and its limitations.