Temperature measurement uncertainty quantification in condition monitoring of critical infrastructure using complex timeseries dependency modeling

Abstract

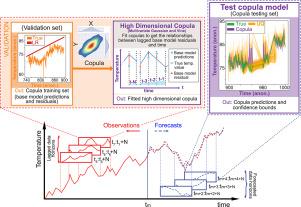
Maintenance interventions are required to keep power generation component temperatures within prescribed guidelines but come with the consequence of lost generation days. Understanding temperature increases caused by asset aging processes is critical to maintain safe operation but avoid needless maintenance. This is particularly important when power plants are approaching the end of their planned operational lifetime and may not operate as efficiently, eroding generation revenue margins. Temperature measurements, in many cases the earliest indicators of performance degradation, can be subject to a variety of uncertainty and noise stemming from plant configuration, sensor calibration changes and the general variability of component aging processes. The capability to provide confidence bounds on the predicted temperatures in the presence of measurement noise can permit maintenance decisions to be made with sufficient certainty on lead time to select the best course of maintenance action, given operational or financial constraints. This paper presents an approach for identifying the rate at which mechanical component temperatures can increase over a given operational horizon and presents a predictive distribution of the predictive error that may result from that estimate. A framework utilizing the dependency structure between propagated measurement and modeling uncertainty is developed through investigating a series of increasingly detailed Copula-based approaches applied to the residuals from data-based predictive models. The contribution is demonstrated on operational power generation data as well as stylized exemplar data.