In-plane bidirectional quasi-static compression behavior of a novel multi-step star-isosceles triangular honeycomb
IF 7.9
2区 材料科学
Q1 MATERIALS SCIENCE, MULTIDISCIPLINARY
引用次数: 0
Abstract
Multi-stage plateau stress structures have recently attracted increasing attention for impact protection and energy absorption. However, most existing designs either provide limited in-plane energy absorption or exhibit multi-stage features only in one loading direction. To address the above-mentioned limitations, this research proposes a novel star-isosceles triangular honeycomb (SITH) structure. It combines the tunability of star-shaped geometries with the stability of triangular frameworks. The mechanical performance of SITH was systematically investigated through quasi-static experiments and numerical simulations. The results show that SITH provides excellent energy absorption in both directions under in-plane biaxial loading. Uniquely, it achieves three plateau stages in the Y direction. A theoretical model was formulated based on the deformation mechanisms that were observed. This model accurately predicts plateau stresses and critical strains. Parametric analyses of the key geometric angles further reveal their influence on the mechanical response. These insights support the optimization of structural performance. Compared with previously reported hybrid honeycombs, the proposed SITH structure demonstrates superior stability, tunable multi-stage energy absorption, and effectiveness in both loading directions. This work establishes a theoretical basis for design of star-shaped hybrid honeycombs. It also offers a promising strategy for impact protection in complex engineering environments.
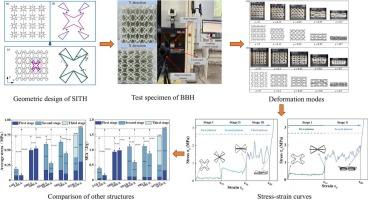
一种新型多阶星形等腰三角形蜂窝的平面内双向准静态压缩行为
近年来,多阶段高原应力结构在保护冲击和吸收能量方面受到越来越多的关注。然而,大多数现有设计要么提供有限的面内能量吸收,要么仅在一个加载方向上表现出多级特征。针对上述局限性,本研究提出了一种新的星形等腰三角形蜂窝(SITH)结构。它结合了星形几何的可调性和三角形框架的稳定性。通过准静态实验和数值模拟,系统地研究了SITH的力学性能。结果表明,在平面内双轴载荷作用下,SITH在两个方向上都具有良好的吸能性能。独特的是,它在Y方向上实现了三个平台阶段。根据观测到的变形机理,建立了理论模型。该模型准确地预测了平台应力和临界应变。关键几何角度的参数分析进一步揭示了它们对力学响应的影响。这些见解支持结构性能的优化。与先前报道的混合蜂窝相比,所提出的SITH结构具有更好的稳定性,多级可调的能量吸收,以及在两个加载方向上的有效性。为星形混合蜂窝的设计奠定了理论基础。为复杂工程环境下的冲击防护提供了一种有前景的策略。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
Materials & Design
Engineering-Mechanical Engineering
CiteScore
14.30
自引率
7.10%
发文量
1028
审稿时长
85 days
期刊介绍:
Materials and Design is a multi-disciplinary journal that publishes original research reports, review articles, and express communications. The journal focuses on studying the structure and properties of inorganic and organic materials, advancements in synthesis, processing, characterization, and testing, the design of materials and engineering systems, and their applications in technology. It aims to bring together various aspects of materials science, engineering, physics, and chemistry.
The journal explores themes ranging from materials to design and aims to reveal the connections between natural and artificial materials, as well as experiment and modeling. Manuscripts submitted to Materials and Design should contain elements of discovery and surprise, as they often contribute new insights into the architecture and function of matter.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


