Bubble dynamics near a rigid boundary with a protruded cone
IF 3.8
2区 工程技术
Q1 MECHANICS
International Journal of Multiphase Flow
Pub Date : 2025-09-23
DOI:10.1016/j.ijmultiphaseflow.2025.105456
引用次数: 0
Abstract
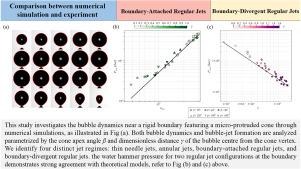
This study investigates bubble dynamics near a rigid boundary consisting of a protruded cone and a plane. This boundary represents irregularly shaped structures or protruding components, often occurring in practical applications. This phenomenon, under an axisymmetric configuration, is investigated through numerical simulations based on the compressible Navier–Stokes equations and the Volume of Fluid (VOF) method, which has been validated for accurately capturing bubble dynamics. Both bubble dynamics and bubble-jet formation are analyzed parameterized by the cone apex angle () and dimensionless distance () of the bubble center from the cone vertex. We identify four distinct jet regimes: thin needle jets, annular jets, boundary-attached regular jets, and boundary-divergent regular jets. Furthermore, the pressure for two regular jet configurations at the boundary demonstrates strong agreement with theoretical models. Notably, an extreme case marked by complete jet suppression is observed.
具有凸锥的刚性边界附近的气泡动力学
本文研究了由凸出的圆锥体和一个平面组成的刚性边界附近的气泡动力学。这个边界代表不规则形状的结构或突出的部件,经常出现在实际应用中。基于可压缩Navier-Stokes方程和流体体积(VOF)方法的数值模拟研究了轴对称构型下的这一现象,并验证了该方法能够准确捕捉气泡动力学。用锥顶点角(β)和气泡中心到锥顶点的无因次距离(γ)对气泡动力学和气泡射流形成进行了分析。我们确定了四种不同的射流模式:细针射流、环形射流、边界附加规则射流和边界发散规则射流。此外,边界处两种规则射流结构的压力与理论模型非常吻合。值得注意的是,观察到一个极端的情况,其标志是完全的射流抑制。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
7.30
自引率
10.50%
发文量
244
审稿时长
4 months
期刊介绍:
The International Journal of Multiphase Flow publishes analytical, numerical and experimental articles of lasting interest. The scope of the journal includes all aspects of mass, momentum and energy exchange phenomena among different phases such as occur in disperse flows, gas–liquid and liquid–liquid flows, flows in porous media, boiling, granular flows and others.
The journal publishes full papers, brief communications and conference announcements.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


