Three-Dimensional Flow of Ideal Fluid with Precessing Vortex Lines (Exact Solutions)
IF 1.3
3区 数学
Q2 MATHEMATICS, APPLIED
引用次数: 0
Abstract
Three-dimensional hydrodynamic equations of ideal incompressible fluid in Lagrangian form are considered. Their explicit solution is obtained. The trajectories of fluid particles are complex spatial curves depending on four frequencies. The vortex lines precess around the vertical axis. Their shape is determined by an arbitrary function depending on the axial Lagrangian coordinate. It is shown that the rotation axis is directed to the plane of vortex lines at some nonzero angle.
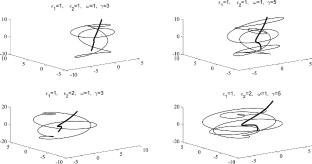
带涡线的理想流体三维流动(精确解)
考虑了理想不可压缩流体拉格朗日形式的三维水动力方程。得到了它们的显式解。流体粒子的轨迹是依赖于四个频率的复杂空间曲线。旋涡线绕垂直轴进动。它们的形状由依赖于轴向拉格朗日坐标的任意函数决定。结果表明,旋转轴以非零角度指向涡线平面。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
2.00
自引率
15.40%
发文量
97
审稿时长
>12 weeks
期刊介绍:
The Journal of Mathematical Fluid Mechanics (JMFM)is a forum for the publication of high-quality peer-reviewed papers on the mathematical theory of fluid mechanics, with special regards to the Navier-Stokes equations. As an important part of that, the journal encourages papers dealing with mathematical aspects of computational theory, as well as with applications in science and engineering. The journal also publishes in related areas of mathematics that have a direct bearing on the mathematical theory of fluid mechanics. All papers will be characterized by originality and mathematical rigor. For a paper to be accepted, it is not enough that it contains original results. In fact, results should be highly relevant to the mathematical theory of fluid mechanics, and meet a wide readership.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


