Thermal Convection in a Higher Velocity Gradient and Higher Temperature Gradient Fluid

Abstract

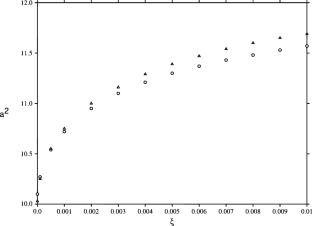
We analyse a model for thermal convection in a class of generalized Navier-Stokes equations containing fourth order spatial derivatives of the velocity and of the temperature. The work generalises the isothermal model of A. Musesti. We derive critical Rayleigh and wavenumbers for the onset of convective fluid motion paying careful attention to the variation of coefficients of the highest derivatives. In addition to linear instability theory we include an analysis of fully nonlinear stability theory. The theory analysed possesses a bi-Laplacian term for the velocity field and also for the temperature field. It was pointed out by E. Fried and M. Gurtin that higher order terms represent micro-length effects and these phenomena are very important in flows in microfluidic situations. We introduce temperature into the theory via a Boussinesq approximation where the density of the body force term is allowed to depend upon temperature to account for buoyancy effects which arise due to expansion of the fluid when this is heated. We analyse a meaningful set of boundary conditions which are introduced by Fried and Gurtin as conditions of strong adherence, and these are crucial to understand the effect of the higher order derivatives upon convective motion in a microfluidic scenario where micro-length effects are paramount. The basic steady state is the one of zero velocity, but in contrast to the classical theory the temperature field is nonlinear in the vertical coordinate. This requires care especially dealing with nonlinear theory and also leads to some novel effects.