Elephant Random Walk with Polynomially Decaying Steps

Abstract

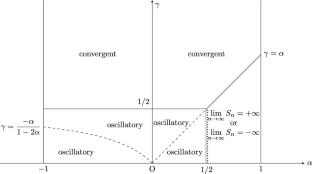
In this paper, we introduce a variation of the elephant random walk whose steps are polynomially decaying. At each time k, the walker’s step size is \(k^{-\gamma }\) with \(\gamma >0\). We investigate effects of the step size exponent \(\gamma \) and the memory parameter \(\alpha \in [-1,1]\) on the long-time behavior of the walker. For fixed \(\alpha \), it admits phase transition from divergence to convergence (localization) at \(\gamma _{c}(\alpha )=\max \{\alpha ,1/2\}\). This means that large enough memory effect can shift the critical point for localization. Moreover, we obtain quantitative limit theorems which provide a detailed picture of the long-time behavior of the walker.