Inverse design of two-dimensional architected materials with desired uniaxial polynomial nonlinear constitutive responses aided by stiffness normalization

Abstract

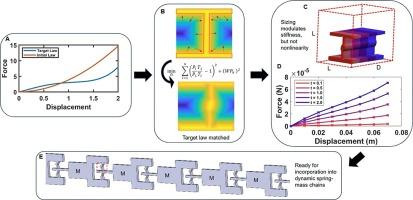
The design of specified nonlinear mechanical responses into a structure or material is a highly sought after capability, with significant potential impacts in areas such as wave tailoring in metamaterials, impact mitigation, soft robotics, and biomedicine. Here, we present a topology optimization approach to design two-dimensional structures for desired uniaxial polynomial nonlinear behavior, wherein we formulate the objective function to match nonlinear coefficient ratios, such that the linear stiffness is decoupled from the desired nonlinearity of the response. We suggest that such linear stiffness decoupling can help aid convergence for problems with fixed, but poorly matched, constituent materials and design volumes. This benefit can be understood by considering, if large absolute force values and stiffnesses are targeted, thicker structures with less open space generally result. Such high volume ratio structures reduce the kinematic freedom (available to, e.g., long thin structures) which is needed for strong geometrically nonlinear responses. We show designs achieved using this approach that match a range of qualitatively different polynomial behaviors with high precision, which are of interest, in particular, within the domain of dynamical systems where nonlinear elasticity of relatively simple polynomial forms can confer greater analytical tractability.