Perspectivity in complemented modular lattices and regular rings
IF 0.6
4区 数学
Q3 MATHEMATICS
引用次数: 0
Abstract
Based on an analogue for systems of partial isomorphisms between lower sections in a complemented modular lattice we construct a series of terms (including inner inverse as basic operation and providing descending chains) such that principal right ideals \(aR \cong bR\) in a (von Neumann) regular ring R are perspective if the series becomes stationary. In particular, this applies if \(aR \cap bR\) is of finite height in L(R). This is used to derive, for existence-varieties \(\mathcal {V}\) of regular rings, equivalence of unit-regularity and direct finiteness, both conceived as a property shared by all members of \(\mathcal {V}\).
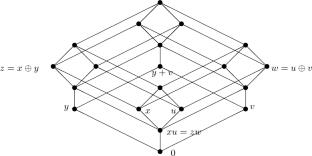
补模格与正则环的透视性
基于对互补模格下截面间的部分同构系统的模拟,我们构造了一系列项(包括作为基本运算的内逆和提供下行链),使得(冯·诺伊曼)正则环R中的主右理想\(aR \cong bR\)在级数变为平稳时是可见的。特别地,这适用于\(aR \cap bR\)在L(R)中的高度有限的情况。这是用来推导,对于正则环的存在变量\(\mathcal {V}\),单位正则性和直接有限性的等价,它们都被认为是\(\mathcal {V}\)的所有成员共有的性质。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Algebra Universalis
数学-数学
CiteScore
1.00
自引率
16.70%
发文量
34
审稿时长
3 months
期刊介绍:
Algebra Universalis publishes papers in universal algebra, lattice theory, and related fields. In a pragmatic way, one could define the areas of interest of the journal as the union of the areas of interest of the members of the Editorial Board. In addition to research papers, we are also interested in publishing high quality survey articles.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


