Accurate analytical post-buckling solutions for simply supported square plates under biaxial compression with varying stress ratios

Abstract

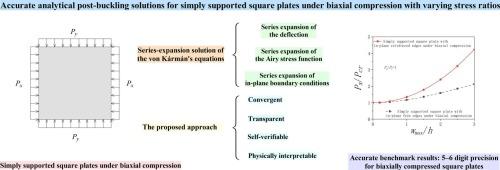
This study addresses the challenge of obtaining accurate analytical post-buckling solutions for simply supported square plates under biaxial compression, a long-standing problem in nonlinear plate mechanics. The research question focuses on how to rigorously capture large deflections and bending–membrane interactions to establish reliable benchmarks beyond the critical load. A series expansion method within the von Kármán framework is employed to derive analytical solutions with high numerical accuracy. Compared with existing analytical and numerical approaches, the present solutions achieve five to six significant digits of accuracy, representing a substantial improvement in precision and reliability. A comprehensive parametric study demonstrates how varying the biaxial compression ratio influences post-buckling responses, providing deeper insight into boundary-sensitive and load-dependent behaviors. The results establish new analytical benchmarks that can be directly used to validate approximate and numerical methods, thereby improving the robustness of computational models. In addition, they offer practical guidance for the safe and efficient design of thin-walled plate structures in aerospace, civil, and mechanical engineering. This work highlights both the novelty of deriving truly accurate, verifiable analytical solutions and their dual value as theoretical milestones and engineering tools.