Impact of anisotropic porosity on electroosmotic flow of micropolar fluid in wavy channel
IF 3.8
2区 工程技术
Q1 MECHANICS
International Journal of Multiphase Flow
Pub Date : 2025-09-11
DOI:10.1016/j.ijmultiphaseflow.2025.105444
引用次数: 0
Abstract
The influence of weak anisotropy on electroosmotic flow of micropolar fluids in geometrically non-uniform microchannels is explored through a comprehensive theoretical framework. Using a rigorous mathematical framework, a comprehensive model is developed that couples the Poisson–Boltzmann equation governing the electric double layer dynamics and the Brinkman equation with the micro rotational term. To tackle this difficulty, the perturbation technique is employed to resolve the coupled equations with appropriate boundary conditions, where the channel’s aspect ratio () is taken as the perturbation parameter. A comprehensive analysis is conducted to examine the effects of critical parameters such as the Debye–Hückel parameter, anisotropic ratio, fluctuation parameter, micro-scale parameter (), and coupling parameter () on various flow characteristics. The findings indicate that a stronger micropolar effect leads to a decrease in linear velocity near the wavy wall, while a contrasting increase in linear velocity is observed at greater distances from the wall. The velocity profiles computed numerically using the finite difference method show negligible difference between solutions from linearized Poisson–Boltzmann equations (Debye–Hückel approximation) and non-linear Poisson–Boltzmann equations for weak anisotropy. These findings have significant implications for optimizing microfluidic devices in biomedical applications, chemical separation processes, and micro-scale heat exchangers where precise flow control is paramount.
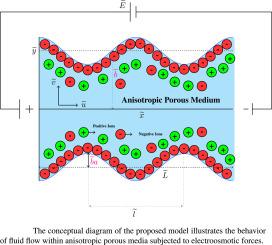
各向异性孔隙度对波浪通道中微极流体电渗透流动的影响
通过一个综合的理论框架,探讨了弱各向异性对微极流体在几何非均匀微通道中电渗透流动的影响。利用严格的数学框架,建立了控制电双层动力学的泊松-玻尔兹曼方程和含微旋转项的布林克曼方程的耦合综合模型。为了解决这一困难,采用了微扰技术来求解具有适当边界条件的耦合方程,其中通道的纵横比(δ≪1)被作为微扰参数。综合分析了debye - hckel参数、各向异性比、波动参数、微尺度参数(m)、耦合参数(N)等关键参数对各种流动特性的影响。研究结果表明,较强的微极效应导致波浪壁附近线速度下降,而在距离波浪壁较远的地方观察到线速度的相反增加。用有限差分法数值计算的速度分布表明,线性化泊松-玻尔兹曼方程(debye - h ckel近似)和非线性泊松-玻尔兹曼方程在弱各向异性下的解之间的差异可以忽略不计。这些发现对优化生物医学应用、化学分离过程和微型热交换器中的微流体装置具有重要意义,其中精确的流量控制至关重要。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
7.30
自引率
10.50%
发文量
244
审稿时长
4 months
期刊介绍:
The International Journal of Multiphase Flow publishes analytical, numerical and experimental articles of lasting interest. The scope of the journal includes all aspects of mass, momentum and energy exchange phenomena among different phases such as occur in disperse flows, gas–liquid and liquid–liquid flows, flows in porous media, boiling, granular flows and others.
The journal publishes full papers, brief communications and conference announcements.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


