Hybrid AutoEncoder/Galerkin approach for nonlinear reduced order modelling

Abstract

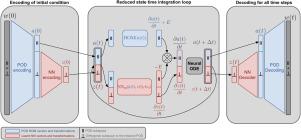
This paper presents a novel nonlinear Reduced Order Model (ROM) that combines Proper Orthogonal Decomposition (POD) with deep learning residual error correction. Deep learning is used for error correction in both the projection and time integration phases of the ROM. This enables simultaneous correction within the POD subspace (error in the reduced subspace) and outside (truncation error). The present hybrid ROM is trained using an end-to-end neural Ordinary Differential Equations (ODE) framework, aligning the deep learning component with the continuous-time nature of the governing equations. We evaluate its performance using well-studied test cases: the viscous Burgers equation, the cylinder flow at a single Reynolds number (equal to 100), as well as for Reynolds numbers ranging from 60 to 120 (parametric cylinder case) and the fluidic pinball in the quasi-periodic regime. These non-chaotic test cases, are chosen to assess different aspects of the method and its ability to accurately predict reproducible dynamics. Our novel strategy outperforms several existing approaches both in terms of accuracy and dimensionality reduction: POD Galerkin ROMs, a purely data-driven approach using only autoencoders, and also state-of-the-art hybrid methods. Furthermore, it offers low computational overhead compared to classical POD-based ROMs, making it attractive for complex 2D or 3D systems.