Non-Fourier heat conduction: Discrete vs continuum approaches

Abstract

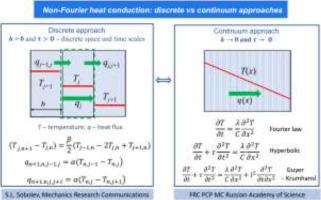
Under far from local-equilibrium conditions, that is on ultra-short space and time scales, the inherent non-locality of the heat conduction process begins to play a crucial role. The discrete variable model (DVM), which assumes that time and space are discrete variables, is one of the most effective approaches to describe the nonlocal effects. Heat conduction equation, energy conservation law, and constitutive equation for the heat flux have been formulated and analyzed in the framework of the DVM. The DVM predicts rather unusual behavior in the spectral characteristics of discrete heat equations on ultrashort time and length scales compared to predictions of continuum approaches. This unusual behavior may serve as a guide for new experimental investigations of high-frequency heat flow regimes, observation of new physical phenomena in solid and thermal materials to expand the range of their technological applications.

To bridge the gap between the discrete and continuum approaches, two invariants for the continualization procedure, namely, thermal diffusivity and propagation velocity of temperature disturbances, have been employed. It has been demonstrated that in the continuum limit the discrete heat equation contains an infinite hierarchy of partial differential equations including classical Fourier, hyperbolic, Guyer-Krumhansl and Jeffreys heat conduction equations. Generalizations of the DVM to two-dimensional and two-temperature cases have been considered. Possible applications of the discrete approach to heat conduction in nano systems and metamaterials have been discussed.