Modeling tracer dispersion in a coupled system composed of a proppant-packed hydraulic fracture and a tight porous medium
IF 4.2
2区 环境科学与生态学
Q1 WATER RESOURCES
引用次数: 0
Abstract
Tracer tests are widely performed for the characterization of reservoir properties during the hydraulic fracturing operation. The dispersion of the tracer depends on the interaction of the proppant-packed hydraulic fracture and the tight porous medium through the naturally porous walls. However, the effects of the interaction of the porous walls and dynamics of flow in the proppant-packed hydraulic fracture on the tracer dispersion and reservoir dynamic mass/heat storage capacity have not yet been reported in the literature. In this work, the tracer dispersion in a proppant-packed hydraulic fracture surrounded by a tight porous medium is theoretically modeled and the dynamic storage capacity is evaluated. The Darcy-Brinkman equation is used to describe the fully developed laminar Stokes fluid flow in the proppant-packed hydraulic fracture. We used the Taylor dispersion theory and Reynolds decomposition approach to derive the exact equivalent transport parameters, including dispersion and advection coefficients, as well as the storage capacity of the tight porous medium. It is found that the tracer dispersion is controlled by the Darcy and the Peclet numbers in the proppant-packed hydraulic fracture. The results indicate that the ratio of tracer dispersion in the proppant-packed hydraulic fracture with porous walls to that with nonporous walls ranges from zero for very small Darcy numbers to 0.3 for large Darcy numbers. The ratio of the advection velocity in the proppant-packed hydraulic fracture with porous walls to that with nonporous walls ranges from unity for very small Darcy numbers to 7/5 for large Darcy numbers. The results also indicate that tracer mass storage capacity in the tight porous medium increases as the Peclet number for fluid flow in the proppant-packed hydraulic fracture increases. Conversely, storage decreases as the Darcy number in the proppant-packed hydraulic fracture rises. A comparison reveals that a flow transport model based on proppant-free hydraulic fracture may lead to the overestimation of the tracer mass/heat storage capacity. The findings of this study pave the way to advance our understanding of tracer tests for evaluating reservoir characteristics during fracturing operations in enhanced geothermal systems.
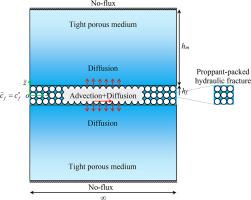
模拟含支撑剂的水力裂缝和致密多孔介质耦合系统中的示踪剂分散
在水力压裂作业中,示踪剂测试被广泛用于表征储层性质。示踪剂的分散取决于支撑剂充填的水力裂缝与穿过天然多孔壁的致密多孔介质的相互作用。然而,在支撑剂充填的水力裂缝中,多孔壁的相互作用和流动动力学对示踪剂分散性和储层动态质量/储热能力的影响尚未在文献中报道。在这项工作中,理论模拟了被致密多孔介质包围的支撑剂填充水力裂缝中的示踪剂分散,并评估了动态存储容量。Darcy-Brinkman方程用于描述支撑剂充填水力裂缝中完全发育的层流Stokes流体流动。我们使用Taylor色散理论和Reynolds分解方法推导出精确的等效输运参数,包括色散和平流系数,以及致密多孔介质的存储容量。研究发现,在充填支撑剂的水力裂缝中,示踪剂的分散受Darcy数和Peclet数的控制。结果表明,在支撑剂填充的水力裂缝中,多孔壁与非多孔壁的示踪剂弥散比在达西数很小时为0,在达西数很大时为0.3。在支撑剂填充的水力裂缝中,多孔壁面的平流速度与无孔壁面的平流速度之比从很小的达西数为1到很大的达西数为7/5不等。结果还表明,随着支撑剂充填水力裂缝中流体流动的Peclet数的增加,致密多孔介质中示踪剂的质量存储容量也随之增加。相反,随着支撑剂充填水力裂缝中达西数的增加,储层会减少。对比表明,基于无支撑剂水力压裂的流动输运模型可能会导致对示踪剂质量/储热能力的高估。这项研究的发现为我们进一步了解在增强型地热系统压裂作业中,用于评估储层特征的示踪测试铺平了道路。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Advances in Water Resources
环境科学-水资源
CiteScore
9.40
自引率
6.40%
发文量
171
审稿时长
36 days
期刊介绍:
Advances in Water Resources provides a forum for the presentation of fundamental scientific advances in the understanding of water resources systems. The scope of Advances in Water Resources includes any combination of theoretical, computational, and experimental approaches used to advance fundamental understanding of surface or subsurface water resources systems or the interaction of these systems with the atmosphere, geosphere, biosphere, and human societies. Manuscripts involving case studies that do not attempt to reach broader conclusions, research on engineering design, applied hydraulics, or water quality and treatment, as well as applications of existing knowledge that do not advance fundamental understanding of hydrological processes, are not appropriate for Advances in Water Resources.
Examples of appropriate topical areas that will be considered include the following:
• Surface and subsurface hydrology
• Hydrometeorology
• Environmental fluid dynamics
• Ecohydrology and ecohydrodynamics
• Multiphase transport phenomena in porous media
• Fluid flow and species transport and reaction processes
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


