Elucidating rubber loading-unloading mechanical response and permanent set using combined hyperelastic-pseudoelastic-viscoelastic/plastic model

Abstract

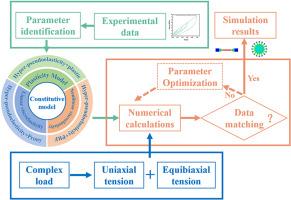
Rubber materials exhibit extremely complex nonlinear mechanical responses under complex actual service conditions such as large deformation and periodic cyclic loading. Using only a hyperelastic constitutive model to describe these responses can significantly deviate from the actual response. A comprehensive understanding of material damage and permanent set behavior is imperative for guiding the design optimization and reliability evaluation of long-life, high-performance rubber components. In this paper, the uniaxial tensile recovery curve of natural rubber (NR)composites and the uniaxial and equibiaxial mode tensile recovery curves of Eucommia ulmoides gum (EUG) composites were obtained through experiments. Three constitutive model combinations (Yeoh hyperelastic model, Ogden-Roxburgh pseudoelastic model and Prony series viscoelastic model/Parallel Rheological Framework model/Plastic model) were used to fit the uniaxial tensile recovery curve of natural rubber composites. Among them, the hyperelastic-pseudoelastic-PRF (Parallel Rheological Framework) nonlinear viscoelastic model showed excellent fitting ability, and the coefficient of determination R² of the fitting result reached 0.995. In order to expand the application scenarios of the hyperelastic-pseudoelastic-PRF model combination, it was applied to the uniaxial and equibiaxial tensile recovery deformation analysis of EUG composites. The results show that the combination of hyperelastic-pseudoelastic-PRF model can achieve high-precision prediction of the loading-unloading mechanical response of rubber under different loading modes, and the coefficient of determination R² of the uniaxial and equibiaxial tensile recovery simulation data exceeds 0.985. By verifying the Drucker stability of the hyperelastic model, this method can provide a solution to the problem that complex nonlinear constitutive equations such as the hyperelastic-pseudoelastic-PRF model combination are difficult to converge in practical applications.