Oscillatory Brinkman-micropolar electroosmosis in cylindrical microannuli
IF 4.6
2区 物理与天体物理
Q1 PHYSICS, MULTIDISCIPLINARY
引用次数: 0
Abstract
This study presents an analytical investigation of unsteady, time-periodic flow in a hydrogel medium confined within a cylindrical microannulus, driven by both a pressure gradient and an externally applied electric field. The hydrogel is modeled as a Brinkman porous matrix saturated with a micropolar fluid. By coupling the linearized Poisson-Boltzmann equation (Debye-Hückel approximation) with the Brinkman-micropolar momentum equations, closed-form expressions are derived for the axial velocity and microrotation as functions of radial position, time, and key dimensionless parameters. The flow is shown to comprise two independent contributions: a pressure-driven component and an electroosmotic component, each influenced by specific physical mechanisms. Quantitatively, increasing the permeability resistance parameter () from 0 to 10 reduces the volume flow rate by 89.64 %, the streaming function by 83.63 %, while increasing microrotation strength by 62.05 %. Raising the micropolar coupling number () from 0.1 to 0.9 leads to a 38.20 % decrease in flow rate, a 165.55 % increase in the streaming function, and a 28.43 % rise in microrotation. Frequency effects are especially pronounced: increasing the forcing frequency parameter () from 0.5 to 50 results in a 99.98 % drop in flow rate, a 100 % increase in the streaming function, and a 99.9997 % rise in microrotation. The electrokinetic width () is a dominant tuning parameter-doubling from 10 to 20 leads to a 581.94 % increase in flow rate, and 315.86 % in the streaming function. The analysis also reveals how zeta potential asymmetry () enables precise flow control, including reversal. All classical limiting cases-Newtonian, purely pressure-driven, and steady electroosmotic-are exactly recovered, validating the model. These findings provide quantitative guidelines for the design of hydrogel-based microfluidic systems where electrokinetic and microstructural effects critically influence transport.
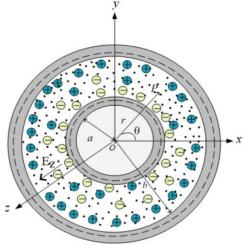
圆柱形微环腔中的振荡布林克曼微极性电渗透
本研究分析了在压力梯度和外加电场驱动下,水凝胶介质在圆柱形微环空中的非定常、时间周期流动。水凝胶的模型是布林克曼多孔基质饱和微极性流体。通过将线性化泊松-玻尔兹曼方程(debye - h ckel近似)与brinkman -微极动量方程耦合,导出了轴向速度和微旋转作为径向位置、时间和关键无量纲参数的函数的封闭表达式。流体由两种独立的贡献组成:压力驱动成分和电渗透成分,每一种成分都受到特定物理机制的影响。从数量上看,将渗透阻力参数λ从0增加到10,使体积流率降低89.64%,流函数降低83.63%,微旋强度提高62.05%。微极耦合数(c)由0.1提高到0.9,流量降低38.20%,流态功能提高165.55%,微旋度提高28.43%。频率效应尤其明显:将强迫频率参数(α)从0.5增加到50,导致流量下降99.98%,流函数增加100%,微旋度增加99.9997%。电动势宽度(k)是一个主要的调节参数,k从10倍增加到20倍,导致流量增加581.94%,流函数增加315.86%。分析还揭示了ζ电位不对称(β≠1)如何实现精确的流量控制,包括反转。所有经典的极限情况-牛顿,纯压力驱动,稳定电渗透-完全恢复,验证了模型。这些发现为基于水凝胶的微流体系统的设计提供了定量指导,其中电动和微观结构效应对传输有重要影响。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Chinese Journal of Physics
物理-物理:综合
CiteScore
8.50
自引率
10.00%
发文量
361
审稿时长
44 days
期刊介绍:
The Chinese Journal of Physics publishes important advances in various branches in physics, including statistical and biophysical physics, condensed matter physics, atomic/molecular physics, optics, particle physics and nuclear physics.
The editors welcome manuscripts on:
-General Physics: Statistical and Quantum Mechanics, etc.-
Gravitation and Astrophysics-
Elementary Particles and Fields-
Nuclear Physics-
Atomic, Molecular, and Optical Physics-
Quantum Information and Quantum Computation-
Fluid Dynamics, Nonlinear Dynamics, Chaos, and Complex Networks-
Plasma and Beam Physics-
Condensed Matter: Structure, etc.-
Condensed Matter: Electronic Properties, etc.-
Polymer, Soft Matter, Biological, and Interdisciplinary Physics.
CJP publishes regular research papers, feature articles and review papers.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


