On linear and nonlinear diffusion in liquids according to linear nonequilibrium thermodynamics

Abstract

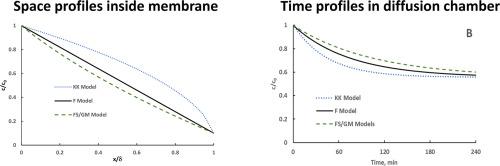
The derivation of the description of diffusive-convective transport from the linear non-equilibrium thermodynamics (LNT) by Kedem and Katchalsky (KK, 1958) yields a nonlinear diffusion equation (with diffusivity parameter proportional to solute concentration) whereas experimental data frequently can be described by the linear equation with constant diffusivity parameter.

Three different assumptions on the dependence of Onsager phenomenological parameters on solute concentrations are applied to derive KK model and two new alternative models. All three models have the same expression for total volumetric flow. The alternative models involve linear free self-diffusion but all three models predict a nonlinear term added to diffusion across osmotically active milieu (as permselective membranes); the cross-diffusion parameters are in general dependent on solute concentration and include the additional nonlinear term valid for osmotically active milieu. A theoretical example of diffusion across a permselective membrane in diffusional chamber allow us for the comparison of the predictions from the different models for ideal diluted solutions. Representations of the solute fluxes using solute volumetric velocities are also derived for each model. The analysis of published experimental data on free diffusion in ternary systems and on the diffusive transport across semipermeable membrane in binary systems, with the measurements of transport parameters for different solute concentrations, using the experimentally established diffusivity parameters and Onsager phenomenological parameters, indicates one of the new models instead of the KK model.

We conclude that the Kedem-Katchalsky approach cannot be confirmed for some experimental systems and another proposed model should be further investigated for the description of solute transport in incompressible fluids.