Inflation of a Circular Hyperelastic Membrane: A Numerical Analysis

Abstract

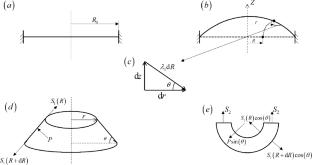
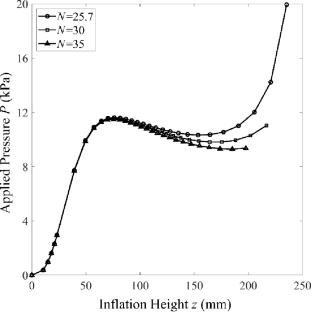
The inflation tests of rubbery membranes have been widely employed as an efficient method to characterize the stress response as biaxial loading states. However, most of the previous theoretical works have employed classic hyperelastic models to analyze the deformation behaviors of inflated membranes. The classic models have been demonstrated to lack the ability to capturing the biaxial deformation of rubbers. To address this issue, we have combined the analytical method and the finite element simulation to investigate the deformation response of soft membranes with different constitutive relationships. For the analytical method, the governing ordinary differential equations have been set up for the boundary value problem of inflation tests and further solved using the shooting method. The analytical results are consistent with those obtained from finite element simulation. The results show that the deformation belongs to the unequal biaxial condition rather than the equi-biaxial state unless a neo-Hookean model is adopted. We also perform a parameter study using the extended eight-chain model, which shows that a change in different parameters affects the mechanical response of inflation tests variously. This work may shed light on the future experimental characterization of soft materials using inflation experiments.