Spacelike Initial Data for Black Hole Stability

Abstract

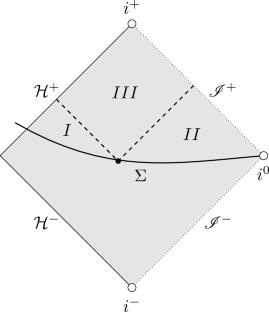
We construct initial data suitable for the Kerr stability conjecture, that is, solutions to the constraint equations on a spacelike hypersurface with boundary entering the black hole horizon that are arbitrarily decaying perturbations of a Kerr initial data set. This results from a more general perturbative construction on any asymptotically flat initial data set with \(r^{-1}\) fall-off and the topology of \(\mathbb {R}^3\setminus \{r<1\}\) enjoying some analyticity near and at the boundary. In particular, we design a suitable mixed boundary condition for the elliptic operator of the conformal method in order to exclude the Killing initial data sets (KIDS).